Variable aleatoria

Una función que asocia un número real, perfectamente definido, a cada punto muestral.

A veces las variables aleatorias (v.a.) están ya implícitas en los puntos muestrales.

Ejemplo 1: Experiencia consistente en medir la presión sistólica de 100 individuos. Un punto muestral (resultado de un experimento) es ya un número (presión sistólica). La v.a. está implícita.

Ejemplo 2: En el ejemplo de la mujer portadora de hemofilia.

W = {sss, ssn, sns, snn, nss, nsn, nns, nnn}

Se podría definir una variable que asignara a cada punto muestral el número de orden en el espacio muestral.

X: sss 1; ssn 2; sns 3;...

Pero otra posible v.a.: a cada punto muestral el número de s. X: sss 3; ssn 2; ...

Los conjuntos pueden ser:

discretos: número finito o infinito numerable de elementos.

continuos: número infinito no numerable de elementos.

Las v.a. definidas sobre espacios muestrales discretos se llaman v.a. discretas y las definidas sobre espacios muestrales continuos se llaman continuas.

Una v.a. puede ser continua, aunque nosotros sólo podamos acceder a un subconjunto finito de valores. P.e. la presión arterial es una v.a. continua pero sólo podemos acceder a un conjunto finito de valores por la limitación de los aparatos de medida.

En general, las medidas dan lugar a v.a. continuas y los conteos a v.a. discretas.

Inducción de la probabilidad a variables aleatorias

Las v.a permiten definir la probabilidad como una función numérica (de variable real) en lugar de como una función de conjunto como se había definido antes

Ejemplo 3: Tiramos una moneda 3 veces. Representamos cara por c y cruz por z.

W = {ccc, ccz, czc, zcc, czz, zcz, zzc, zzz}

La probabilidad de cada suceso elemental es 1/8. Por ejemplo p(ccc)=1/8, ya que la probabilidad de sacar cara en una tirada es 1/2 según la definición clásica y las tiradas son independientes.

Definimos la v.a. X: número de caras, que puede tomar los valores {0, 1, 2, 3}. Se buscan todos los puntos muestrales que dan lugar a cada valor de la variable y a ese valor se le asigna la probabilidad del suceso correspondiente.

A esta función se le denomina función densidad de probabilidad (fdp), que desgraciadamente "funciona" de distinta manera en las variables discreta que en las continuas. En el caso de las variables discretas, como en el ejemplo, es una función que para cada valor de la variable da su probabilidad.

Ejemplo 4: Supongamos la variable tipo histológico de un tumor, con los valores 1, 2, 3, 4. Si la fdp fuera

significaría que la probabilidad del tipo 2 es 0,27, etc.

Para variables continuas la probabilidad de que una variable tome cualquier valor concreto es 0, por lo tanto la fdp sólo permite calcular la probabilidad para un intervalo del tipo (a<X<b), mediante el área bajo la curva de la fdp.

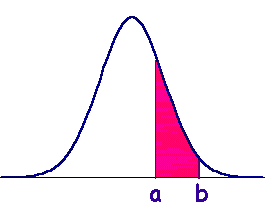
Para las variables aleatorias de interés hay tablas, y programas de ordenador, donde buscar esos valores.

Distribución acumulativa o función de distribución

F(x) = p(X £ x)

Para el ejemplo 3

y para el ejemplo 4

Parámetros característicos de una fdp

Valor esperado o esperanza matemática o media

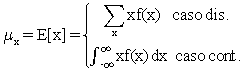
si X es una v.a. cualquier función de ella, h(x), es también una v.a., en consecuencia también se define este parámetro para una función de v.a.

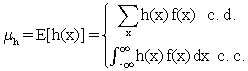
Ejemplo 5: Se tira un dado. Se define como v.a. el número que sale ¿Cuál es su media?

La variable X puede tomar los valores 1, 2, ..., 6 y para todos ellos f(x) = 1/6. En consecuencia la media es

Observese que es un número que la v.a. no puede alcanzar. ¿Qué significa? No mucho.

Se define ahora una función sobre X: el premio: si sale 1 ó 2 se gana 100 ptas, si sale 3 se gana 500 y si sale 4, 5 ó 6 no se gana nada

¿Cuál es el valor medio de esta función?

¿qué significa? es el valor medio a la larga: si se juega un número grande de veces la ganancia final es como si en cada jugada se hubiera ganado 116,6 pts. Si la apuesta costara menos de eso el juego sería ventajoso para el jugador (así se enriqueció Voltaire), si costara más, para la banca. (llamar a ésto honestidad del juego le costó el puesto de ministro a Laplace).

Varianza:

Se define como:

aunque para el cálculo se suele usar esta otra fórmula equivalente:

¿Qué mide la varianza? Mide la dispersión de la variable alrededor de la media.

Otras lecturas recomendadas

Variables and parameters. Altman & Bland. BMJ 1999; 318:1667.