Como
los estimadores de Kaplan-Meier
son estimadores de máxima verosimilitud y la teoría establece que estos
estimadores son asintóticamente normales, una primera aproximación es
usar dicha teoría, es decir, si de una población con función de supervivencia
S(t) se extraen dos muestras independientes, y a partir de las
mismas se calculan los estimadores 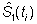 y
y 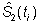 debido a su normalidad asintótica, las variables:
debido a su normalidad asintótica, las variables:
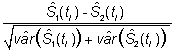
son, también asintóticamente, normales de media 0 y varianza 1. Estas variables se pueden usar para comparar para cada tiempo predeterminado, las dos estimaciones. Sin embargo, generalmente, no interesa comparar para un tiempo predeterminado (a veces sí, por ejemplo para tiempos de corte muy establecidos como supervivencia a los 5 años para el cáncer), sino comparar globalmente ambas curvas de supervivencia.
Evidentemente,
se podrían comparar, por este procedimiento, punto a punto, pero este
modo de proceder es poco eficiente ya que no se usan todos los datos en
cada comparación y aparecen los problemas asociados a las comparaciones
múltiples y, en consecuencia, se han desarrollado pruebas para realizar
una única comparación global. La más popular es la conocida como prueba
del log-rank y puede verse como una aplicación de la prueba de
Mantel y Haenszel para tablas de contingencia estratificadas y que se
puede generalizar a la comparación de r funciones de supervivencia,
con un estadístico que se distribuye como una c2
con r - 1 grados de libertad.
Ejemplo 2
Compárense las funciones de supervivencia para los datos siguientes; donde, como en el ejemplo anterior, las pérdidas están indicadas con asteriscos; extraídos de dos muestras hipotéticas correspondientes a dos tratamientos distintos.
trat. A: 10, 13, 15*, 17, 19*, 20*
trat. B: 8, 10, 11, 11*, 12, 15*
Para hacerlo con el SPSS, se necesita crear un archivo con tres variables: tiempo, estado (codificado, por ejemplo, 0: pérdida, 1: muerte) y tratamiento (codificado, por ejemplo, 0: tratamiento A, 1: tratamiento B).
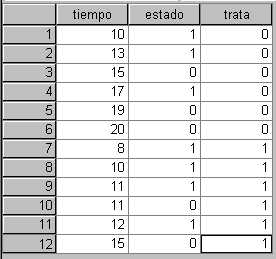
y el resultado
Survival Analysis for TIEMPOFactor TRATA = A
| Time | Status | Cumulative Survival |
Standard Error |
Cumulative
Events |
Number Remaining |
| 10 | muerte | ,8333 | ,1521 | 1 | 5 |
| 13 | muerte | ,6667 | ,1925 | 2 | 4 |
| 15 | pérdida | 2 | 3 | ||
| 17 | muerte | ,4444 | ,2222 | 3 | 2 |
| 19 | pérdida | 3 | 1 | ||
| 20 | pérdida | 3 | 0 |
Number of Cases: 6 Censored: 3 ( 50,00%) Events: 3
| Survival Time |
Standard Error |
95%
Confidence Interval |
|
| Mean: (Limited to 20) |
17 | 2 | ( 13; 20 ) |
| Median: | 17 | 4 | ( 9; 25 ) |
Survival Analysis for TIEMPO
Factor TRATA = B
| Time | Status | Cumulative Survival |
Standard Error |
Cumulative
Events |
Number Remaining |
| 8 | muerte | ,8333 | ,1521 | 1 | 5 |
| 10 | muerte | ,6667 | ,1925 | 2 | 4 |
| 11 | muerte | ,5000 | ,2041 | 3 | 3 |
| 11 | pérdida | 3 | 2 | ||
| 12 | muerte | ,2500 | ,2041 | 4 | 1 |
| 15 | pérdida | 4 | 0 |
Number of Cases: 6 Censored: 2 ( 50,00%) Events: 4
| Survival Time |
Standard Error |
95%
Confidence Interval |
|
| Mean: (Limited to 15) |
12 | 1 | ( 10; 14 ) |
| Median: | 11 | 1 | ( 9; 13 ) |
Survival Analysis for TIEMPO
| Total | Number Events |
Number Censored |
Percent Censored |
|
| TRATA A | 6 | 3 | 3 | 50,00 |
| TRATA B | 6 | 4 | 2 | 33,00 |
| OVERALL | 12 | 7 | 5 | 41,67 |
Test Statistics for Equality of Survival Distributions for TRATA
| Statistic | df | Significance | |
| Log Rank | 2,23 | 1 | ,1352 |
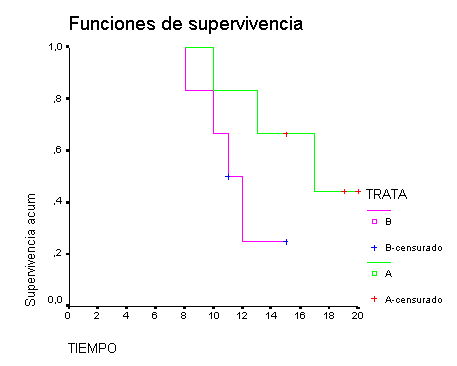
O con AlcEst para ver los intervalos de confianza
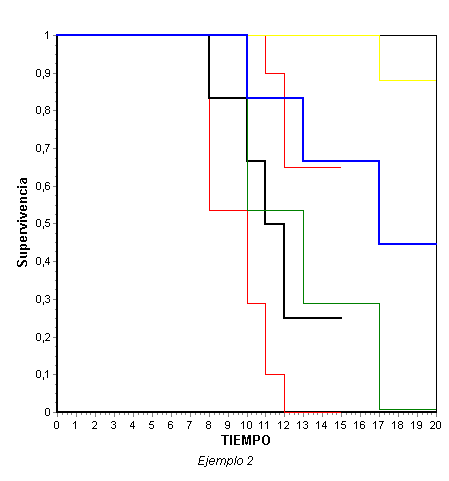
Ejemplo 3
Se quiere comparar la supervivencia a una cierta intervención quirúrgica en 3 hospitales distintos. Para ello se sigue en cada hospital a una muestra aleatoria de pacientes intervenidos (habitualmente, y para aumentar el tamaño muestral, se sigue a todos los intervenidos, considerándolos entonces una muestra de todos los potenciales enfermos) y se obtienen los siguientes tiempos, en meses:
Hosp A: 1, 3, 7, 8*, 12, 12, 15*
Hosp B: 2, 2, 3, 8, 10, 10, 12*, 15
Hosp C: 1, 1, 3, 7, 10*, 12, 12, 14, 15*
El resultado es:
Survival Analysis for TIEMPOFactor HOSPITAL = A
| Time | Status | Cumulative Survival |
Standard Error |
Cumulative
Events |
Number Remaining |
| 1 | muerte | ,8571 | ,1323 | 1 | 6 |
| 3 | muerte | ,7143 | ,1707 | 2 | 5 |
| 7 | muerte | ,5714 | ,1870 | 3 | 4 |
| 8 | pérdida | 3 | 3 | ||
| 12 | muerte | 4 | 2 | ||
| 12 | muerte | ,1905 | ,1676 | 5 | 1 |
| 15 | pérdida | 5 | 0 |
Number of Cases: 7 Censored: 2 ( 28,57%) Events: 5
| Survival Time |
Standard Error |
95%
Confidence Interval |
|
| Mean: (Limited to 15) |
9 | 2 | ( 5; 13 ) |
| Median: | 12 | 2 | ( 8; 16 ) |
Survival Analysis for TIEMPO
Factor HOSPITAL = B
| Time | Status | Cumulative Survival |
Standard Error |
Cumulative
Events |
Number Remaining |
| 2 | muerte | 1 | 7 | ||
| 2 | muerte | ,7500 | ,1531 | 2 | 6 |
| 3 | muerte | ,6250 | ,1712 | 3 | 5 |
| 8 | muerte | ,5000 | ,1768 | 4 | 4 |
| 10 | muerte | 5 | 3 | ||
| 10 | muerte | ,2500 | ,1531 | 6 | 2 |
| 12 | pérdida | 6 | 1 | ||
| 15 | muerte | ,0000 | ,0000 | 7 | 0 |
Number of Cases: 8 Censored: 1 ( 12,50%) Events: 7
| Survival Time |
Standard Error |
95%
Confidence Interval |
|
| Mean: | 8 | 2 | ( 4; 12 ) |
| Median: | 8 | 3 | ( 2; 14 ) |
Survival Analysis for TIEMPO
Factor HOSPITAL = C
| Time | Status | Cumulative Survival |
Standard Error |
Cumulative
Events |
Number Remaining |
| 1 | muerte | 1 | 8 | ||
| 1 | muerte | ,7778 | ,1386 | 2 | 7 |
| 3 | muerte | ,6667 | ,1571 | 3 | 6 |
| 7 | muerte | ,5556 | ,1656 | 4 | 5 |
| 10 | pérdida | 4 | 4 | ||
| 12 | muerte | 5 | 3 | ||
| 12 | muerte | ,2778 | ,1617 | 6 | 2 |
| 14 | muerte | ,1389 | ,1272 | 7 | 1 |
| 15 | pérdida | 7 | 0 |
Number of Cases: 9 Censored: 2 ( 22,22%) Events: 7
| Survival Time |
Standard Error |
95%
Confidence Interval |
|
| Mean: (Limited to 15) |
9 | 2 | ( 5; 12 ) |
| Median: | 12 | 3 | ( 6; 18 ) |
Survival Analysis for TIEMPO
| Total | Number Events |
Number Censored |
Percent Censored |
|
| HOSPITAL A | 7 | 5 | 2 | 28,57 |
| HOSPITAL B | 8 | 7 | 1 | 12,50 |
| HOSPITAL C | 9 | 7 | 2 | 22,22 |
| OVERALL | 24 | 19 | 5 | 20,83 |
Test Statistics for Equality of Survival Distributions for TRATA
| Statistic | df | Significance | |
| Log Rank | ,41 | 2 | ,8164 |
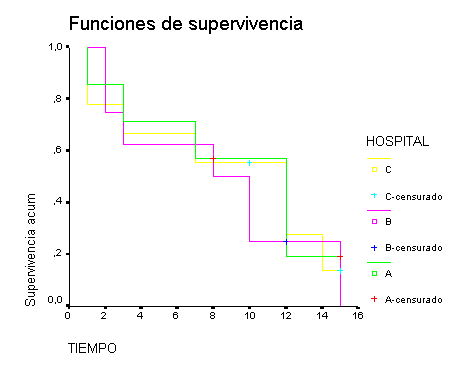
|
|
|
|
|
