Modelo de regresión de Poisson

Para una única variable independiente X, es un modelo de la forma:

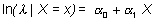
o, para simplificar la notación, simplemente:

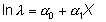
donde ln significa logaritmo neperiano, a₀ y a₁ son constantes y X una variable que puede ser aleatoria o no, continua o discreta. Este modelo se puede fácilmente generalizar para k variables independientes:

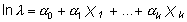
Por lo tanto a₀ es el logaritmo de l (probabilidad de que ocurra un evento en un intervalo de tamaño unidad) cuando todas las variables independientes son cero, y a_i es el cambio en el logaritmo de l (o logaritmo del cociente de l ) cuando la variable X_i aumenta una unidad, manteniéndose constantes las demás o, dicho de otro modo, 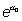es la probabilidad de que ocurra un evento en un intervalo unidad cuando todas las variables independientes son cero y 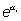l el cociente de dicha probabilidad para un aumento de una unidad en la variable X_i (riesgo relativo). Obsérvese que, al igual que en la regresión logística, el modelo supone efectos multiplicativos, es decir, si la variable X_i aumenta n unidades, la probabilidad para la variable de Poisson se multiplica por 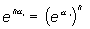es decir, la potencia n-ésima de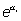

Teniendo en cuenta, que para una variable de Poisson: m = ls el modelo también se puede poner en función de m como:

Ejemplo

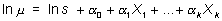
Se quiere comparar la incidencia de cáncer de piel en 2 ciudades, para ello se registran los cánceres de piel aparecidos en el último año, 18 para la ciudad A y 30 para la B, cuyas poblaciones respectivas son 350.000 y 410.000.

Se trata de variables de Poisson con intervalo de personas-tiempo. Asumiendo que ambas poblaciones se han mantenido constantes a lo largo de ese año y que todos los individuos eran susceptibles de enfermar, los tamaños de los intervalos son respectivamente 350.000 y 410.000 personas-año y la mejor estimación de las densidades de incidencia:

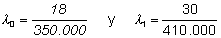
Definiendo la variable X = 0 para la ciudad A y X = 1 para la B, estos resultados se pueden expresar con un modelo de regresión, siendo:

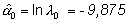
el logaritmo de la densidad de incidencia en la ciudad A y 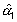el logaritmo de la razón de densidades de incidencia, es decir:

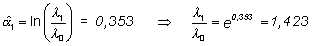
Por lo tanto, la densidad de incidencia en B es 1,423 la de A (42,3% más alta). Evidentemente, para comparar ambas incidencias, simplemente hay que comparar 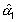con cero o 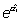con 1.

Se puede plantear que esta diferencia en las incidencias pueda ser debida, simplemente, a que ambas ciudades tengan una distinta pirámide de población (es sabido que la incidencia del cáncer es distinta para distintos grupos de edad) o quizás, y sería una hipótesis más interesante a investigar, a algún otro factor. Si se conoce la distribución de las poblaciones para los distintos grupos de edad, así como el grupo al que pertenece cada enfermo, se puede plantear un modelo:

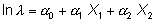
siendo X₁ la ciudad y X₂ el grupo de edad. En este modelo a₁ es la razón de densidades de incidencia para ambas ciudades controlando por la edad. Si a₁ es distinto de 0, se puede concluir que existe algún factor, distinto de la edad, en ambas ciudades que incide en el cáncer de piel.