Concordancia para variables continuas
Aunque en la literatura clínica hay una gran tradición de usar el coeficiente de correlación lineal (r) para evaluar la concordancia entre variables continuas, ello es incorrecto: dicho coeficiente mide la correlación y no la concordancia: si, p.e. un aparato para medir una magnitud produce sistemáticamente el triple de otro aparato que supuestamente mide la misma magnitud, ambas mediciones están perfectamente correlacionadas (r=1) pero no son concordantes en absoluto.
Ejemplo: en 1979, en un artículo de gran impacto entre neumólogos (Thorax,34:807-809), se comparaba las medidas de flujo respiratorio máximo obtenidas por el aparato estándar (Wright) con las obtenidas por otro portátil (miniWright). Los autores hacen hincapié en que ambas medidas se correlacionaban muy bien (r=0,992) y proponen el uso alternativo del portátil. Como veremos enseguida las cosas no eran tan claras.
El índice más establecido para variables continuas es el denominado coeficiente de correlación intraclase que se calcula a partir de los estadísticos que produce un análisis de la varianza y que, por tanto, no estamos en condiciones de abordar en este curso.
Un procedimiento, gráfico, alternativo propuesto por Altman e ilustrado con datos del estudio anterior es el siguiente:
| Paciente | Wright (l/min) | MiniWright (l/min) | Diferencia | Media |
| 1 | 494 | 512 | -18 | 503.0 |
| 2 | 395 | 430 | -35 | 412.5 |
| 3 | 516 | 520 | -4 | 518.0 |
| 4 | 434 | 428 | 6 | 431.0 |
| 5 | 476 | 500 | -24 | 488.0 |
| 6 | 557 | 600 | -43 | 578.5 |
| 7 | 413 | 364 | 49 | 388.5 |
| 8 | 442 | 380 | 62 | 411.0 |
| 9 | 650 | 658 | -8 | 654.0 |
| 10 | 433 | 445 | -12 | 439.0 |
| 11 | 417 | 432 | -15 | 424.5 |
| 12 | 656 | 626 | 30 | 641.0 |
| 13 | 267 | 260 | 7 | 263.5 |
| 14 | 478 | 477 | 1 | 477.5 |
| 15 | 178 | 259 | -81 | 218.5 |
| 16 | 423 | 350 | 73 | 386.5 |
| 17 | 427 | 451 | -24 | 439.0 |
Si calculamos el coeficiente de correlación lineal
| P R E S T A PC V2.2 | 23-MAR-1995 |
| REGRESION LINEAL |
|
| X = wright MWRIGH |
|
| Y = wright WRIGHT |
|
| NO. DE PUNTOS | 17 |
| COEF. CORRELACION | .943 |
| COEF. DETERMINACION | .890 |
| ERROR ESTANDAR DE LA ESTIMA | 39.882 |
| Ecuación de la recta | Y = .970 X + 11.482 |
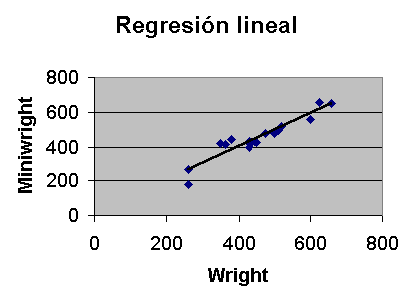La propuesta de Altman es presentar las diferencias contra la media.
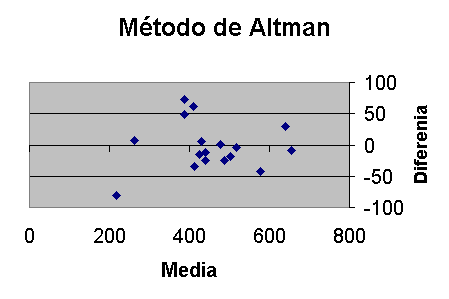
donde se observa que las mediciones no son tan concordantes como parecía en la gráfica anterior.
La media de las diferencias es de -2.1 l/min, es decir hay un error sistemático "hacia abajo" por parte del miniWright. Los límites de concordancia son los límites de confianza de esta diferencia, para calcularlos se calcula la desviación típica de la diferencia, en este caso 38,8 y como t17 =2,11, los límites de concordancia son 79,3 y -83,5, es decir con un 95% de probabilidad la medición del miniWright puede ser 83,5 por debajo o 79,3 por arriba de la media de ambas ¿es esto aceptable clínicamente?
Notar que en la gráfica, las diferencias se mantienen homogéneas a lo largo del eje X. Si no fuera así, este método no se puede usar.
Puesto que estamos trabajando con una muestra, se deben también calcular los límites de confianza para dichos límites de concordancia. El error estándar para estos límites es aproximadamente 
En nuestro caso para el límite inferior serían -114,3 y -45,1 y para el superior 40,9 y 110,1.
Referencias
Bland J.M., Altman D.G. (1986) Statistical methods for assessing agreement between two methods of clinical measurement. Lancet i: 307-310.
Latour J., Abraira V., Cabello J.B., López Sánchez J. (1997) Métodos de investigación en cardiología clínica (IV). Las mediciones clínicas en cardiología: validez y errores de medición. Rev Esp Cardiol 50:117-128.
 |
 |
 |
 |