Usando resultados asintóticos (para grandes muestras) de la teoría de estimación por máxima verosimilitud se obtiene que la varianza de los estimadores de la función de riesgo es
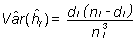
y a partir de aquí, una expresión aproximada para la varianza de la función de supervivencia es (fórmula de Greenwood)
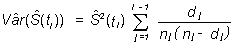
Teniendo en cuenta la normalidad asintótica de los estimadores de máxima verosimilitud, se pueden calcular intervalos de confianza al (1 – α )% para estas estimaciones:
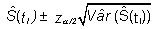
Por ejemplo, para los datos del ejemplo 1, las varianzas de las estimaciones de la función de supervivencia y los intervalos de confianza al 95% construidos con ellas son:
| Tiempo | F. superv. | Varianza | >Intervalo de confianza | |
| 6 | 0,7500 | 0,0156 | 0,9950 | 0,5050 |
| 10 | 0,6563 | 0,0197 | 0,9310 | 0,3815 |
| 12 | 0,5625 | 0,0220 | 0,8530 | 0,2720 |
| 15 | 0,4500 | 0,0242 | 0,7548 | 0,1452 |
| 17 | 0,3000 | 0,0257 | 0,6145 | -0,0145 |
| 22 | 0,0000 | - | - | - |
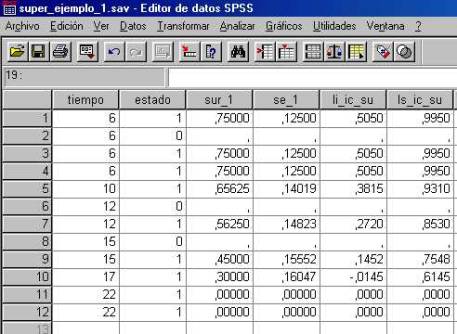
En la “salida” del SPSS figura, en lugar de la varianza, su raíz cuadrada (el error estándar), que es posible guardar en una nueva variable del archivo para, a partir de ella y la función de supervivencia construir los intervalos de confianza.
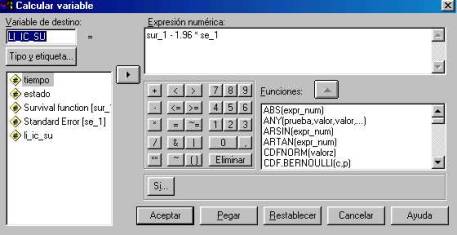
y se obtiene
Una representación gráfica de la función de supervivencia y su intervalo de confianza (obtenida con el programa AlcEst) es
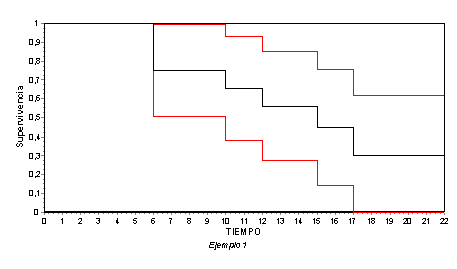
Obsérvese que cuando para un tiempo
ocurre el evento para todos los individuos en riesgo, como en este caso para 22,
la varianza está indeterminada (aunque el SPSS pone 0) puesto que el
denominador es 0. Por otro lado, en los tiempos extremos el intervalo de
confianza puede sobrepasar el intervalo [0,1], en este caso en el tiempo 17.
Ello es debido a que la fórmula de la varianza es sólo aproximada y a que la
normalidad es asintótica. Este problema se puede evitar usando una
transformación logarítmica de
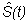 de normalidad también asintótica pero cuyo campo de variación
es todo el campo real.
de normalidad también asintótica pero cuyo campo de variación
es todo el campo real.
A partir de la función
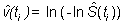
cuyo varianza es
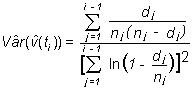
se construyen los intervalos de confianza para S(ti)
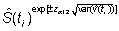
para los datos del ejemplo 1 por este procedimiento se obtienen los intervalos de confianza al 95% dados en la siguiente tabla:
| Tiempo | F. superv. | Varianza | Intervalo de confianza | |
| 6 | 0,7500 | 0,0156 | 0,9117 | 0,4084 |
| 10 | 0,6563 | 0,0197 | 0,8557 | 0,3204 |
| 12 | 0,5625 | 0,0220 | 0,7910 | 0,2437 |
| 15 | 0,4500 | 0,0242 | 0,7104 | 0,1549 |
| 17 | 0,3000 | 0,0257 | 0,6041 | 0,0564 |
| 22 | 0,0000 | - | - | - |
|
|
|
|
|
