La función de Weibull está definida por:
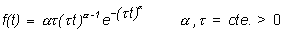
Obsérvese que para a =1 esta función es la exponencial, es decir la función exponencial es una particularización de la función más general de Weibull.
Usando las relaciones entre las tres funciones las funciones de supervivencia y riesgo para esta variable son
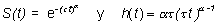
es decir, el riesgo es creciente a lo largo del tiempo para a > 1 (por ejemplo, supervivencia de pacientes con una enfermedad crónica sin respuesta al tratamiento, o materiales con fatiga), constante para a = 1 (materiales sin fatiga) y decreciente para a < 1 (enfermos con cirugía mayor practicada con éxito).
Nótese que calculando dos veces el logaritmo de la función de supervivencia
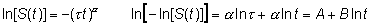
y calculando el logaritmo de la función de riesgo
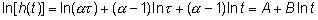
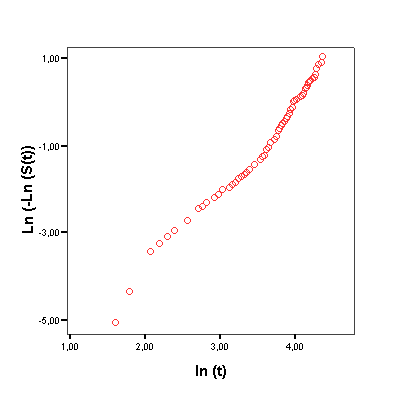
es decir las relaciones entre el logaritmo del logaritmo cambiado de signo de la supervivencia con el logaritmo del tiempo (primera fórmula) y el logaritmo del riesgo con el logaritmo del tiempo (segunda fórmula) son lineales. A veces se usan estas relaciones para evaluar la idoneidad del modelo de Weibull.
Se ha usado esta función para estudiar supervivencia a las bacteriemias y al cáncer gástrico (1).
Ejemplo 6
Ajústese, con las pruebas de bondad de ajuste, la función de Weibull a los datos de la tabla, donde en la columna “Perdida” figura 0 para muerte y 1 para pérdida y en “Tiempo” el tiempo en meses.
La grafica de ln[-ln(S(t))] en función de lnt para evaluar la idoneidad del modelo (en un modelo Weibull debe ser una línea recta).
La salida del PRESTA para este problema (nótese que se denomina parámetro A a t y parámetro B a a
P R E S T A PC V2.2 25-OCT-2001ANALISIS DE SUPERVIVENCIA
MODELO WEIBULL : S(t)=exp[-(At)**B]
NOMBRE DE LOS DATOS: super6
VARIABLE TIEMPO: TIEMPO
VARIABLE PERDIDAS: PERDID
NUMERO DE CASOS: 161
CASOS QUITADOS POR CONTENER ALGUN VALOR NO ESPECIFICADO: 0
| PARAMETRO | ERROR STANDARD | |
| A | .01778 | .00068 |
| B | 2.37622 | .17212 |
MATRIZ DE COVARIANZAS
| A | B | |
| A | .00000 | -.00001 |
| B | -.00001 | .02963 |
LOGARITMO DE MAXIMA VEROSIMILITUD SIN MODELO -516.180700
LOGARITMO DE MAXIMA VEROSIMILITUD DEL MODELO -569.802800
JI-CUADRADO: 107.24410 G.L.: 59 p= .000130
TABLA DE VALORES OBSERVADOS Y ESPERADOS
(SOLO CUENTAN LOS EVENTOS)
| INTERVALO | OBSERVADOS | ESPERADOS | CONT. JI2 |
| < 21.82 | 20.00 | 16.10 | .9447 |
| 21.82 - 29.92 | 8.00 | 16.10 | 4.0752 |
| 29.92 - 36.45 | 10.00 | 16.10 | 2.3112 |
| 36.45 - 42.40 | 13.00 | 16.10 | .5969 |
| 42.40 - 48.21 | 17.00 | 16.10 | .0503 |
| 48.21 - 54.22 | 20.00 | 16.10 | .9447 |
| 54.22 - 60.82 | 5.00 | 16.10 | 7.6528 |
| 60.82 - 68.73 | 14.00 | 16.10 | .2739 |
| 68.73 - 79.91 | 10.00 | 16.10 | 2.3112 |
| > 79.91 | 5.00 | 16.10 | 7.6528 |
PRUEBA DE BONDAD DE AJUSTE
JI-CUADRADO: 26.81367 G.L.: 7 p= .000408
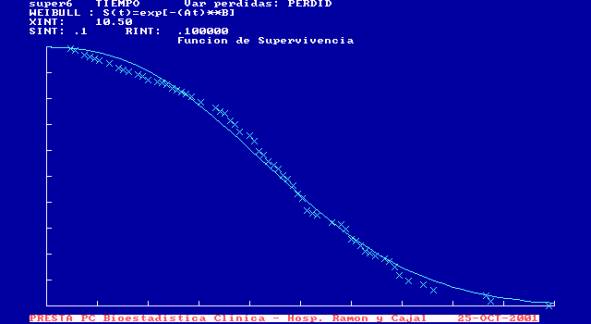
Vuelve a aparecer, como en el ejemplo 4, discrepancias entre ambas pruebas de bondad de ajuste, debido a que en la última no se usan las pérdidas. En estos casos resulta útil recurrir a las pruebas gráficas. Tanto en la gráfica logarítmica como en la comparación de la función de supervivencia con las estimaciones puntuales que se presenta a continuación el modelo parece adecuado.
Un contraste que también interesa hacer es sí el modelo exponencial es adecuado, es decir si a =1 contra la hipótesis alternativa a >1. Se hace con el estadístico
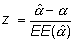
que en este ejemplo es
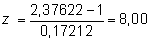
que comparándolo con el valor crítico z0,05= 1,64 permite rechazar la hipótesis nula de modelo exponencial.
ReferenciasMarubini E, Bonfanti G, Bozzetti F, et al. A prognostic score for patients resected for gastric cancer. Eur J Cancer 29A: 845-850. (1993).
|
|
|
|
|
