La función exponencial está definida por:

Usando las relaciones entre las tres funciones las funciones de supervivencia y riesgo para esta variable son
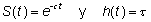
es decir, el riesgo es constante a lo largo del tiempo. A esta propiedad característica de la función exponencial se le suele llamar pérdida de memoria, y es la propiedad que permite evaluar gráficamente si la función exponencial es un modelo adecuado para unos datos.
Si un proceso es de Poisson (suceso raro y aleatorio en el tiempo), la variable “tiempo hasta que ocurra el primer suceso” es exponencial, por esta razón esta función es muy usada en control de calidad donde se puede asumir procesos Poisson (p.e. la vida de los componentes electrónicos en un aparato, el tiempo de espera en una consulta sin cita previa, o la vida de los vasos de vidrio en un bar, siguen esta distribución) y poco en Ciencias de la Salud, aunque se ha usado, por ejemplo, para estudiar supervivencia a la arteritis(1).
Es útil que señalar que, dentro de esta relación
entre las funciones exponencial y de Poisson, el parámetro
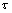 es la media de la variable de Poisson “número de sucesos en la unidad de tiempo”.
es la media de la variable de Poisson “número de sucesos en la unidad de tiempo”.
El estimador del parámetro de la función y su varianza son
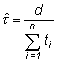
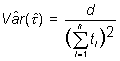
siendo d el número de eventos observados
Calcúlese para los datos del ejemplo 1 la función de supervivencia estimada, asumiendo un modelo exponencial, y realícese la prueba para la bondad del ajuste.
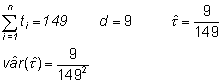
La salida de un paquete estadístico (PRESTA), eligiendo 4 intervalos para la prueba de la bondad de ajuste es:
P R E S T A PC V2.2 19-OCT-2001ANALISIS DE SUPERVIVENCIA
MODELO EXPONENCIAL : S(t)=exp(-At)
NOMBRE DE LOS DATOS: eje1sup
VARIABLE TIEMPO: TIEMPO
VARIABLE PERDIDAS: PERDID
NUMERO DE CASOS: 12
CASOS QUITADOS POR CONTENER ALGUN VALOR NO ESPECIFICADO: 0
| PARAMETRO | ERROR STANDARD | |
| A | .06040 | .02013 |
LOGARITMO DE MAXIMA VEROSIMILITUD SIN MODELO -17.044550
LOGARITMO DE MAXIMA VEROSIMILITUD DEL MODELO -34.260490
JI-CUADRADO: 34.43188 G.L.: 4 p= .000001
TABLA DE VALORES OBSERVADOS Y ESPERADOS
(SOLO CUENTAN LOS EVENTOS)
| INTERVALO | OBSERVADOS | ESPERADOS | CONT. JI2 |
| < 4.76 | .00 | 3.00 | 3.0000 |
| 4.76 - 11.78 | 4.00 | 3.00 | .3333 |
| 11.78 - 22.95 | 5.00 | 3.00 | 1.3333 |
| > 22.95 | .00 | 3.00 | 3.0000 |
PRUEBA DE BONDAD DE AJUSTE
JI-CUADRADO: 7.66667 G.L.: 2 p= .021258
Obsérvese la discrepancia entre ambas pruebas de bondad de ajuste, debido al pequeño tamaño muestral del ejemplo y al hecho de que hay 3 pérdidas cuya información no se usa en la última prueba.
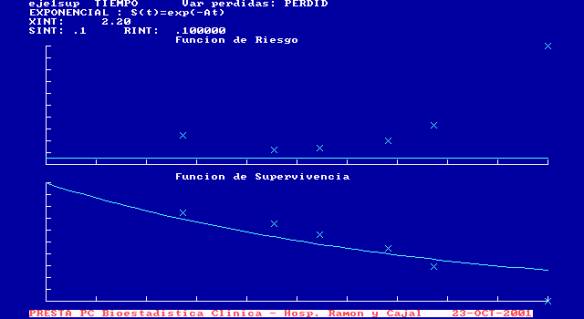
En
la gráfica se muestran las funciones de riesgo y supervivencia asumiendo
el modelo exponencial (línea continua) y las estimaciones puntuales obtenidas
por el método de Kaplan-Meier (aspas).
Visualmente se observa que el modelo no es satisfactorio: las estimaciones
puntuales de la función de riesgo están muy alejadas de la recta horizontal
que corresponde al modelo exponencial.
Compárese, usando el modelo exponencial, las funciones de supervivencia para los datos de la tabla, donde en la columna “Perdida” figura 0 para muerte y 1 para pérdida, en “Trata” 1 y 2 para indicar dos tratamientos distintos y en “Tiempo” el tiempo en meses. Además figura la edad en años al comienzo del tratamiento, que se usará más adelante.
La salida del PRESTA para este problema
P R E S T A PC V2.2 19-OCT-2001ANALISIS DE SUPERVIVENCIA
MODELO EXPONENCIAL : S(t)=exp(-At)
NOMBRE DE LOS DATOS: super5
VARIABLE TIEMPO: TIEMPO
VARIABLE PERDIDAS: PERDID
VARIABLE DEFINE GRUPOS: TRATA
GRUPO 1 Desde 1.00 Hasta 1.00
GRUPO 2 Desde 2.00 Hasta 2.00
NUMERO DE CASOS: 230
CASOS QUITADOS POR CONTENER ALGUN VALOR NO ESPECIFICADO: 0
GRUPO 1
| PARAMETRO | ERROR STANDARD | |
| A | .04826 | .00464 |
LOGARITMO DE MAXIMA VEROSIMILITUD SIN MODELO -387.955200
LOGARITMO DE MAXIMA VEROSIMILITUD DEL MODELO -435.370300
JI-CUADRADO: 94.83020 G.L.: 42 p= .000006
TABLA DE VALORES OBSERVADOS Y ESPERADOS
(SOLO CUENTAN LOS EVENTOS)
| INTERVALO | OBSERVADOS | ESPERADOS | CONT. JI2 |
| < 1.98 | 5.00 | 10.64 | 2.9868 |
| 1.98 - 4.16 | 17.00 | 10.64 | 3.8073 |
| 4.16 - 6.60 | 10.00 | 10.64 | .0381 |
| 6.60 - 9.37 | 9.00 | 10.64 | .2517 |
| 9.37 - 12.56 | 13.00 | 10.64 | .5253 |
| 12.56 - 16.34 | 7.00 | 10.64 | 1.2432 |
| 16.34 - 20.96 | 10.00 | 10.64 | .0381 |
| 20.96 - 26.92 | 8.00 | 10.64 | .6535 |
| 26.92 - 35.33 | 11.00 | 10.64 | .0124 |
| 35.33 - 49.69 | 9.00 | 10.64 | .2517 |
| > 49.69 | 9.00 | 10.64 | .2517 |
PRUEBA DE BONDAD DE AJUSTE
JI-CUADRADO: 10.05983 G.L.: 9 p= .345439
GRUPO 2
| PARAMETRO | ERROR STANDARD | |
| A | .08935 | .00876 |
LOGARITMO DE MAXIMA VEROSIMILITUD SIN MODELO -327.473200
LOGARITMO DE MAXIMA VEROSIMILITUD DEL MODELO -355.183600
JI-CUADRADO: 55.42084 G.L.: 30 p= .003227
TABLA DE VALORES OBSERVADOS Y ESPERADOS
(SOLO CUENTAN LOS EVENTOS)
| INTERVALO | OBSERVADOS | ESPERADOS | CONT. JI2 |
| < 1.07 | 6.00 | 10.27 | 1.7772 |
| 1.07 - 2.25 | 13.00 | 10.27 | .7241 |
| 2.25 - 3.56 | 9.00 | 10.27 | .1577 |
| 3.56 - 5.06 | 12.00 | 10.27 | .2904 |
| 5.06 - 6.78 | 11.00 | 10.27 | .0515 |
| 6.78 - 8.82 | 4.00 | 10.27 | 3.8302 |
| 8.82 - 11.32 | 8.00 | 10.27 | .5028 |
| 11.32 - 14.54 | 13.00 | 10.27 | .7241 |
| 14.54 - 19.08 | 12.00 | 10.27 | .2904 |
| 19.08 - 26.84 | 9.00 | 10.27 | .1577 |
| > 26.84 | 7.00 | 10.27 | 1.0426 |
PRUEBA DE BONDAD DE AJUSTE
JI-CUADRADO: 9.54867 G.L.: 9 p= .388265
Ahora, con un tamaño muestral mayor no hay discrepancia entre ambas pruebas para la bondad del ajuste, las dos indican un buen ajuste. En la figura se presentan las gráficas (líneas continuas: estimaciones de las funciones usando el modelo exponencial y aspas y cuadrados: el método de Kaplan-Meier) y se observa que el ajuste es muy satisfactorio.
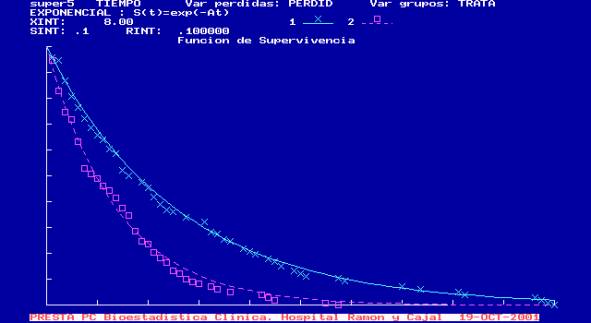
Es decir, con ambos tratamientos el modelo
exponencial es adecuado, o sea el riesgo se mantiene constante a lo largo del
tiempo, siendo 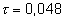 para el tratamiento 1 y
para el tratamiento 1 y 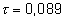 para el 2, dicho de otro modo, con el tratamiento 1 se producen en promedio 0,048
fallecimientos al mes y con el 2 se producen 0,089. Para comparar las curvas se
puede usar la diferencia de los parámetros estimados como estadístico para el
contraste, ya que su distribución muestral es asintóticamente normal con media
0 y varianza la suma de varianzas. En este caso:
para el 2, dicho de otro modo, con el tratamiento 1 se producen en promedio 0,048
fallecimientos al mes y con el 2 se producen 0,089. Para comparar las curvas se
puede usar la diferencia de los parámetros estimados como estadístico para el
contraste, ya que su distribución muestral es asintóticamente normal con media
0 y varianza la suma de varianzas. En este caso:
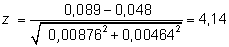
que comparándolo con el valor crítico z0,025= 1,96 permite rechazar la hipótesis nula de igualdad.
ReferenciasM.A.González-Gay, R.Blanco, V.Abraira, C.García-Porrúa, D.Ibáñez, M.T.Rigueiro, A.Sánchez-Andrade, J.Guerrero, E.Casariego. Giant cell arteritis in Lugo, Spain, is associated with low longterm mortality. Journal of Reumathology.24:2171-2176. (1997).
|
|
|
|
|
