La variable T sigue una distribución lognormal si lnT tiene una distribución normal de media μ y varianza σ². En consecuencia, la variable
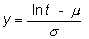
es un variable normal reducida, es decir de media igual a 0 y desviación típica igual a 1. Por lo tanto, la función de supervivencia se puede escribir
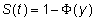
siendo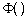 
la función de distribución acumulativa de la
normal reducida. Por lo tanto un modo gráfico de verificar esta distribución es
comparar la función de supervivencia dibujada en papel lognormal con una recta.
La función están caracterizadas por los dos parámetros μ y σ, que no son su media y desviación típica. La estimación de estos parámetros sólo es sencilla en el caso de que no haya pérdidas y ésta es la que implementa el PRESTA.
Se
ha usado esta función para estudiar tanto la supervivencia en SIDA (1),
como el tiempo hasta la seroconversión de HIV+ (2).
Estímese las función de supervivencia, asumiendo el modelo lognormal y realícese la prueba de la bondad de ajuste, para los datos de la tabla.
La salida del PRESTA es (nótese que se denomina parámetro A a m y parámetro B a s2
P R E S T A PC V2.2 25-OCT-2001ANALISIS DE SUPERVIVENCIA
MODELO LOG-NORMAL : f(lnt)=N(A,B)
NOMBRE DE LOS DATOS: super72
VARIABLE TIEMPO: TIEMPO
VARIABLE PERDIDAS NO SE USA
NUMERO
DE CASOS: 121
CASOS QUITADOS POR CONTENER
ALGUN VALOR NO ESPECIFICADO: 0
| PARAMETRO | ERROR STANDARD | |
| A | 2.32263 | .04138 |
| B | .20719 | .02664 |
MATRIZ DE COVARIANZAS
| A | B | |
| A | .00171 | .00000 |
| B | .00000 | .00071 |
TABLA DE VALORES OBSERVADOS Y ESPERADOS
(SOLO CUENTAN LOS EVENTOS)
| INTERVALO | OBSERVADOS | ESPERADOS | CONT. JI2 |
| < 5.69 | 10.00 | 12.10 | .3645 |
| 5.69 - 6.96 | 9.00 | 12.10 | .7942 |
| 6.96 - 8.04 | 18.00 | 12.10 | 2.8769 |
| 8.04 - 9.09 | 12.00 | 12.10 | .0008 |
| 9.09 - 10.20 | 17.00 | 12.10 | 1.9843 |
| 10.20 - 11.45 | 12.00 | 12.10 | .0008 |
| 11.45 - 12.95 | 8.00 | 12.10 | 1.3893 |
| 12.95 - 14.96 | 9.00 | 12.10 | .7942 |
| 14.96 - 18.28 | 16.00 | 12.10 | 1.2570 |
| > 18.28 | 10.00 | 12.10 | .3645 |
PRUEBA DE BONDAD DE AJUSTE
JI-CUADRADO: 9.82645 G.L.: 7 p= .197686
Con la prueba de bondad de ajuste basada en la ji-cuadrado, que en este caso que no hay pérdidas “funciona” mejor, no se rechaza la hipótesis nula de modelo lognormal y en la gráfica también se observa que el modelo es satisfactorio.
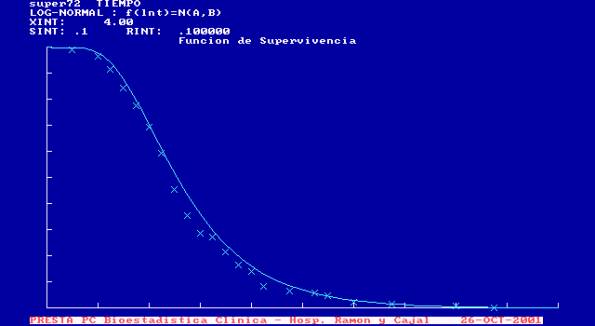
Aceptando que el modelo es bueno, calcúlese la supervivencia a 8 años (suponiendo los tiempos en años) y la mediana de supervivencia.
En la gráfica se observa que para T=8, S(t) es aproximadamente 0,7 y que S(t)=0,5 para t=10 aproximadamente. O bien, más laborioso pero más preciso, usando las fórmulas
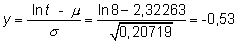
y mirando en la tabla de la normal
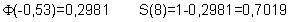
es decir la probabilidad de supervivencia a los 8 años es 0,7019. La mediana es el tiempo en el que S(t)=0,5
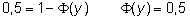
y mirando en la tabla de la normal
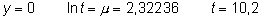
Referencias
-
Veugelers PJ, Cornelisse PG, Craib KJ, et al. Models of survival in HIV infection and their use in the quantification of treatment benefits. Am J Epidemiol 148: 487-496. (1998).
-
Muñoz A, Xu J. Models for the incubation of AIDS and variations according to age and period. Stat Med. 30: 2459-2473. (1996).
|
|
|
|