El modelo gamma está definido por la función de probabilidad
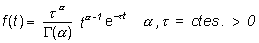
siendo G(a) la función gamma, definida como:
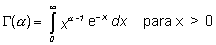
Como G(1) = 1, la función de probabilidad gamma cuando a = 1 es la exponencial. Otro caso particular de esta función es t = 1/2 y a = r/2, siendo r un número natural, que recibe el nombre de ji-cuadrado con r grados de libertad. Del mismo modo que la variable “tiempo hasta que ocurra el primer evento” de un proceso es de Poisson es exponencial, la variable “tiempo hasta que ocurra el evento k-ésimo” es gamma con a = k
La estimación de esta función sólo es sencilla en el caso de que no haya pérdidas y ésta es la que implementa el PRESTA.
Ejemplo 8
Estímese la función de supervivencia, asumiendo el modelo gamma, y realícese la prueba de la bondad de ajuste, para los datos de la tabla.
La salida del PRESTA es (nótese que se denomina parámetro A a a y parámetro B a t )
P R E S T A PC V2.2 27-OCT-2001ANALISIS DE SUPERVIVENCIA
MODELO GAMMA : S(t)=1-I(A,Bt)*(Bt)**A/G(A)
NOMBRE DE LOS DATOS: super8
VARIABLE TIEMPO: TIEMPO
VARIABLE PERDIDAS NO SE USA
NUMERO DE CASOS: 95
CASOS QUITADOS POR CONTENER ALGUN VALOR NO ESPECIFICADO: 0
| PARAMETRO | ERROR STANDARD | |
| A | 7.84341 | .85924 |
| B | .08169 | .00947 |
MATRIZ DE COVARIANZAS
| A | B | |
| A | .73829 | .00772 |
| B | .00772 | .00009 |
LOGARITMO DE MAXIMA VEROSIMILITUD SIN MODELO -388.936400
LOGARITMO DE MAXIMA VEROSIMILITUD DEL MODELO -460.552600
JI-CUADRADO: 143.23240 G.L.: 64 p= .000000
TABLA DE VALORES OBSERVADOS Y ESPERADOS
(SOLO CUENTAN LOS EVENTOS)
| INTERVALO | OBSERVADOS | ESPERADOS | CONT. JI2 |
| < 17.80 | .00 | .02 | .0182 |
| 17.80 - 35.60 | 1.00 | 1.15 | .0205 |
| 35.60 - 53.40 | 6.00 | 7.07 | .1621 |
| 53.40 - 71.20 | 17.00 | 15.81 | .0901 |
| 71.20 - 89.00 | 19.00 | 20.45 | .1023 |
| 89.00 - 106.80 | 17.00 | 18.87 | .1846 |
| 106.80 - 124.60 | 19.00 | 13.86 | 1.9044 |
| 124.60 - 142.40 | 8.00 | 8.65 | .0485 |
| 142.40 - 160.20 | 5.00 | 4.77 | .0110 |
| > 160.20 | 3.00 | 4.36 | .4233 |
PRUEBA DE BONDAD DE AJUSTE
JI-CUADRADO: 2.96491 G.L.: 7 p= .888640
Con ambas pruebas de bondad de ajuste se acepta el modelo gamma y en la gráfica también se observa que el modelo es satisfactorio.
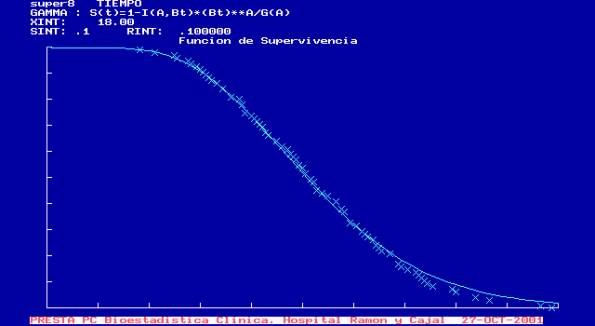
Igual que con el modelo de Weibull, un contraste que también interesa hacer es sí el modelo exponencial es adecuado, es decir si a =1 contra la hipótesis alternativa a >1. Se hace con el estadístico
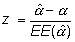
que en este ejemplo es
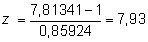
que comparándolo con el valor crítico z0,05= 1,64 permite rechazar la hipótesis nula de modelo exponencial.
|
|
|
|
|
