Curvas ROC
En la clase anterior se consideró que el resultado de las pruebas diagnósticas era categórico, sin embargo muchas pruebas producen resultados continuos, p.e. nivel de glucosa en sangre para diagnosticar la diabetes. El comportamiento de dichas pruebas depende de donde se ponga el punto de corte y lo habitual es que exista un grado variable de solapamiento en la fdp de la variable resultado. En el caso de la glucosa la situación se esquematiza en la gráfica
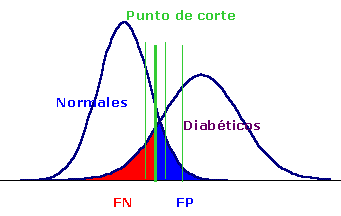
Si se desplaza el punto de corte a la derecha (valores mayores de glucosa) disminuyen los falsos positivos (región azul) pero aumentan los falsos negativos (región roja) o, en otros términos, disminuye la sensibilidad y aumenta la especificidad e inversamente si se desplaza a la izquierda, de modo que un problema en estas pruebas es la selección del punto de corte óptimo. Para caracterizar su comportamiento se usan las llamadas curvas ROC (Receiver Operating Characteristic) desarrolladas por los operadores de radar e introducidas en la investigación clínica por los radiólogos (Hanley y McNeil): son curvas en las que se presenta la sensibilidad en función de los falsos positivos (complementario de la especificidad) para distintos puntos de corte.
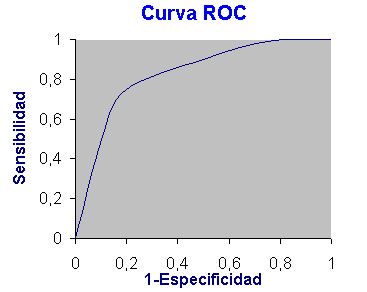
Información contenida en la curva:
- Si la prueba fuera perfecta, es decir, sin solapamiento, hay una región en la que cualquier punto de corte tiene sensibilidad y especifidad iguales a 1: la curva sólo tiene el punto (0,1).
- Si la prueba fuera inútil: ambas fdp´s coinciden y la sensibilidad (verdaderos positivos) es igual a la proporción de falsos positivos, la curva sería la diagonal de (0,0) a (1,1).
- Las pruebas habituales tienen curvas intermedias.
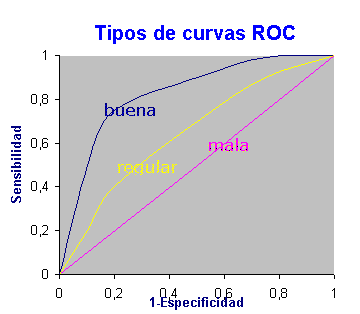
Un parámetro para evaluar la bondad de la prueba es el área bajo la curva que tomará valores entre 1 (prueba perfecta) y 0,5 (prueba inútil). Puede demostrarse, (Hanley y McNeil) que este área puede interpretarse como la probabilidad de que ante un par de individuos, uno enfermo y el otro sano, la prueba los clasifique correctamente.
En
consecuencia, las
curvas ROC son útiles
para:
![]() Conocer el rendimiento global
de una prueba. Area bajo la curva.
Conocer el rendimiento global
de una prueba. Area bajo la curva.
![]() Comparar dos pruebas o dos puntos
de corte. Comparación de dos curvas o de dos puntos sobre una curva.
Comparar dos pruebas o dos puntos
de corte. Comparación de dos curvas o de dos puntos sobre una curva.
![]() Elegir el punto de corte apropiado
para un determinado paciente.
Elegir el punto de corte apropiado
para un determinado paciente.
Limitaciones de su uso: sólo contemplan dos estados clínicos posibles (sano, enfermo) y no sirven para situaciones en que se trata de discernir entre más de dos enfermedades.
Ejemplo: Evaluación del volúmen corpuscular medio (VCM) en el diagnóstico de anemia ferropénica. Se usa como "patrón de oro" la existencia de depósitos de hierro en la médula ósea
Tabla de datos (hipotética):
VCM
Sin Fe (n=34): 52, 58, 62, 65, 67, 68, 69, 71, 72, 72, 73, 73, 74, 75, 76, 77, 77, 78, 79, 80, 80, 81, 81, 81, 82, 83, 84, 85, 85, 86, 88, 88, 90, 92
Con Fe (n=66): 60, 66, 68, 69, 71, 71, 73, 74, 74, 74, 76, 77, 77, 77, 77, 78, 78, 79, 79, 80, 80, 81, 81, 81, 82, 82, 83, 83, 83, 83, 83, 83, 83, 84, 84, 84, 84, 85, 85, 86, 86, 86, 87, 88, 88, 88, 89, 89, 89, 90, 90, 91, 91, 92, 93, 93, 93, 94, 94, 94, 94, 96, 97, 98, 100, 103
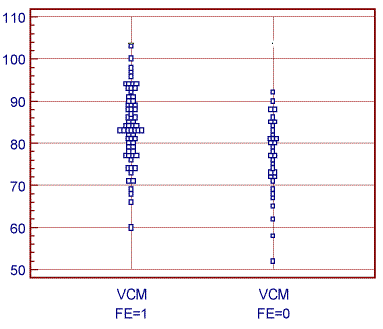
Donde se observa solapamiento. Para diversos puntos de corte (es decir, decidiendo que hay anemia cuando el VCM es menor que el punto de corte) las sensibilidad y proporciones de falsos positivos figuran en la siguiente tabla:
| Punto Corte | Sensibilidad | 1-Especificidad |
| 65 | 3/34=0,088 | 1/66=0,015 |
| 70 | 7/34=0,206 | 4/66=0,061 |
| 75 | 13/34=0,382 | 10/66=0,152 |
| 80 | 19/34=0,559 | 19/66=0,288 |
| 85 | 27/34=0,794 | 37/66=0,561 |
| 90 | 32/34=0,941 | 49/66=0,742 |
| 92 | 33/34=0,971 | 53/66=0,803 |
que producen la siguiente curva ROC
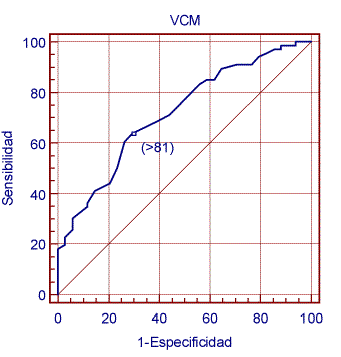
cuya área es 0,717 con un EE de 0,05, es decir no es una prueba demasiado buena. Si se quisiera comparar esta prueba con otra, p.e. niveles séricos de ferritina, se contruiría para ella otra curva y se calcularía su área. Supongamos A=0,868 y EE(A)=0,04. El estadístico para compararlas es (si ambas curvas han sido estimadas independientemente, es decir con distintos sujetos, en caso contrario, véase Hanley J.A., McNeil B.J. (1983)):
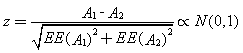
que en este ejemplo vale 2,34 que como es mayor que 1,96 ambas pruebas tienen un rendimiento significativamente distinto.
Referencias
Hanley J.A., McNeil B.J. (1982) The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 143: 29-36
Hanley J.A., McNeil B.J. (1983) A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology. 148: 839-43
|
|
|
|
|
