Distribución muestral de medias

Si tenemos una muestra aleatoria de una población N(m,s ), se sabe (Teorema del límite central) que la fdp de la media muestral es también normal con media m y varianza s²/n. Esto es exacto para poblaciones normales y aproximado (buena aproximación con n>30) para poblaciones cualesquiera. Es decir es el error típico, o error estándar de la media.

¿Cómo usamos esto en nuestro problema de estimación?
1º problema: No hay tablas para cualquier normal, sólo para la normal m=0 y s=1 (la llamada z); pero haciendo la transformación (llamada tipificación)

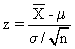
una normal de media m y desviación s se transforma en una z.

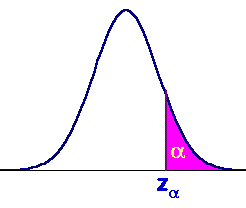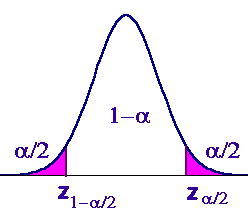
Llamando za al valor de una variable normal tipificada que deja a su derecha un área bajo la curva de a, es decir, que la probabilidad que la variable sea mayor que ese valor es a (estos son los valores que ofrece la tabla de la normal)

podremos construir intervalos de la forma 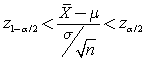para los que la probabilidad es 1 - a.

Teniendo en cuenta la simetría de la normal y manipulando algebraícamente

que también se puede escribir

o, haciendo énfasis en que es el error estándar de la media,

Recuérdese que la probabilidad de que m esté en este intervalo es 1 - a. A un intervalo de este tipo se le denomina intervalo de confianza con un nivel de confianza del 100(1 - a)%, o nivel de significación de 100a%. El nivel de confianza habitual es el 95%, en cuyo caso a=0,05 y z_{a /2}=1,96. Al valor se le denomina estimación puntual y se dice que es un estimador de m.

Ejemplo: Si de una población normal con varianza 4 se extrae una muestra aleatoria de tamaño 20 en la que se calcula se puede decir que m tiene una probabilidad de 0,95 de estar comprendida en el intervalo

que sería el intervalo de confianza al 95% para m

En general esto es poco útil, en los casos en que no se conoce m tampoco suele conocerse s²; en el caso más realista de s² desconocida los intervalos de confianza se construyen con la t de Student (otra fdp continua para la que hay tablas) en lugar de la z.

o, haciendo énfasis en que es el error estándar estimado de la media,

Este manera de construir los intervalos de confianza sólo es válido si la variable es normal. Cuando n es grande (>30) se puede sustituir t por z sin mucho error.

Otras lecturas recomendadas

Interpreting study results: confidence intervals. Guyatt et al. CMAJ. 152:169-173. 1995