Clasificaciones multinomiales
Si bien las clasificaciones binomiales son muy frecuentes, a menudo en clínica resultan insuficientes. P.e. un psiquiatra clasifica los trastornos de los pacientes en psicóticos, neuróticos u orgánicos, o un reumatólogo clasifica las artritis en leves, moderadas o graves. Ambas clasificaciones son multinomiales (tres categorías), no obstante existe una diferencia entre ellas, las categorías en el caso de la artritis pueden ordenarse de un modo relevante para el problema: una artritis grave es más que una moderada, y ésta más que una leve, mientras que para la clasificación psiquiátrica este orden no existe. A las variables multinomiales que tienen implícito un orden se les denomina ordinales y a las que no, nominales. Para estudiar la precisión de una clasificación multinomial, hay ciertas diferencias según que ésta sea ordinal o nominal.
Como en las clasificaciones binarias, los resultados de un estudio de concordancia se pueden resumir en una tabla de doble entrada, aunque ahora con K filas y K columnas, siendo K el número de categorías de la clasificación.
La notación usada en esta tabla es: para identificar una celda se usan dos subíndices: el primero para la fila y el segundo para la columna, por lo tanto Xij es el número de individuos que el observador B ha clasificado en la categoría i y el observador A en la j.
| Observador A | |||||
| Obs. B | Cat. 1 | Cat. 2 | ... | Cat. K | Total |
| Cat. 1 | X11 | X12 | ... | X1K | X1. |
| Cat. 2 | X21 | X22 | ... | X2K | X2. |
| . | . | . | ... | . | . |
| Cat. K | XK1 | XK2 | ... | XKK | XK. |
| Total | X.1 | X.2 | ... | X.K | N |
Para indicar los totales marginales se usa un punto en el lugar del subíndice con respecto al que se ha sumado: Xi. es la suma de la fila i y X.j es la suma de la columna j. En notación algebraica

Para una clasificación multinomial se puede definir un índice kappa idéntico al anterior, generalizando el cálculo de Po y Pe como
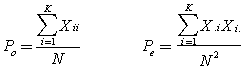
Ejemplo: Dos reumatólogos clasifican en tres categorías (leve, moderada, grave) 80 enfermos con artritis. Los resultados son
| Reumatólogo A | ||||
| Reum. B | Leve | Mode. | Grave | Total |
| Leve | 9 | 8 | 3 | 20 |
| Moderada | 9 | 29 | 5 | 43 |
| Grave | 0 | 3 | 14 | 17 |
| Total | 18 | 40 | 22 | 80 |
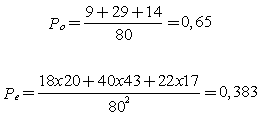
![]()
Otra alternativa para estudiar concordancia entre clasificaciones multinomiales consiste en definir un índice kappa para cada una de las categorías, colapsando la tabla KxK original en K tablas 2x2 en las que se compara cada categoría con todas las demás. De este modo se puede estudiar la contribución de cada una de ellas a la concordancia de la clasificación.
Para los datos del ejemplo, se colapsaría la tabla en 3 tablas: una comparando la categoría leve con las demás, otra la moderada con las demás y la tercera la grave con las otras.
| 1 | 2 | 3 | |||||||
| Obs A | Obs A | Obs A | |||||||
| L | O | M | O | G | O | ||||
| Obs B | L | 9 | 11 | M |
29 | 14 |
G |
14 | 3 |
| O | 9 | 51 | O |
11 | 26 |
O |
8 | 55 | |
L: leve, M: moderada, G:grave, O:otra.
calculando en cada una de estas tablas Po, Pe y k resulta:
| tabla | Po | Pe | k |
| 1 | 0,75 | 0,638 | 0,309 |
| 2 | 0,688 | 0,5 | 0,376 |
| 3 | 0,863 | 0,629 | 0,631 |
donde se observa que la clasificación de la categoría grave es la que mayor k produce (¿Cómo se interpreta?).
|
|
|
|
|
