Comparación de modelos pronósticos.

Con frecuencia es necesario realizar la comparación entre un nuevo modelo pronóstico  con otro ya existente; para ello se han propuesto diversos índices, entre ellos el índice de mejoría de la discriminación, IDI (Integrated Discrimination Improvement) y el índice de mejoría de la reclasificación, NRI (Net Reclassification Improvement) propuestos por Pencina et al. [1] para la situación en que a un modelo existente se le añade una nueva variable, aunque no hay inconveniente en aplicarlos a la comparación de dos modelos más generales, siempre que se puedan aplicar los dos a una misma muestra.

Índice de mejoría de la discriminación: IDI.

El IDI se define como la diferencia de las medias de las probabilidades del evento, estimadas por los modelos nuevo y viejo en los pacientes que hacen evento, menos la misma diferencia en aquellos que no hacen evento:

Donde  es la media de las probabilidades predichas del evento por el nuevo modelo, en los pacientes que hacen evento;  es la media de las probabilidades predichas del evento por el viejo modelo, en los pacientes que hacen evento, etc. Es decir, el IDI representa lo que mejora en promedio el nuevo modelo en cuanto a la predicción de más verdaderos eventos, descontando lo que empeora por la predicción de falsos eventos.

Asumiendo independencia entre eventos y no eventos y sus probabilidades predichas, se puede calcular una prueba asintótica de la hipótesis nula de IDI=0.

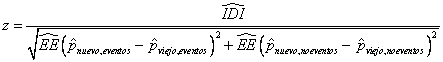
Esta prueba se puede implementar muy fácilmente con cualquier paquete estadístico. Por ejemplo, con SPSS habría que  guardar las probabilidades predichas de los 2 modelos logísticos (viejo y nuevo), calcular su diferencia y comparar, mediante la prueba T de Student para muestras independientes, las medias de estas diferencias entre eventos y no eventos.

Un programa que lo genera, suponiendo que en el archivo de datos la variable evento se llame “EVENTO” y está codificada como 1=”sí” y 0=”no”, las variables del modelo viejo se llamen X1, X2, X3, X4 y en el modelo nuevo se añadan X5, X6, es:

LOGISTIC REGRESSION VARIABLES EVENTO
  /METHOD=ENTER X1 X2 X3 X4
  /SAVE=PRED(PVIEJA)
  /CRITERIA=PIN(.05) POUT(.10) ITERATE(20) CUT(.5).

* la probabilidad predicha se guarda en “PVIEJA”

LOGISTIC REGRESSION VARIABLES EVENTO
  /METHOD=ENTER X1 X2 X3 X4 X5 X6
  /SAVE=PRED(PNUEVA)
  /CRITERIA=PIN(.05) POUT(.10) ITERATE(20) CUT(.5).

* la probabilidad predicha se guarda en “PNUEVA”

COMPUTE DIFPRE=PNUEVA - PVIEJA.
EXECUTE.

* la diferencia se guarda en “DIFPRE”

T-TEST GROUPS=EVENTO(1 0)
  /MISSING=ANALYSIS
  /VARIABLES=DIFPRE
  /CRITERIA=CI(.95).

Que produce la salida:

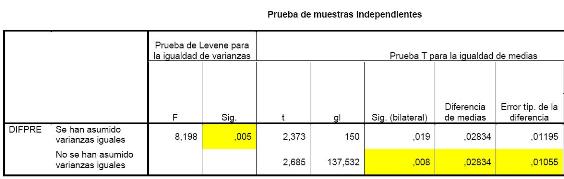
En ella, la diferencia de medias (0,02834) es el IDI, su error estándar, que aparece en el denominador de la fórmula de Pencina, es el que corresponde a “No se han asumido varianzas iguales” (0,01055), pero podría usarse el correspondiente a “Se han asumido varianzas iguales” (0,01195) si el valor p de la prueba de Levene lo permitiera (>0,05).

Índice de mejoría de la reclasificación: NRI

El NRI exige categorizar las probabilidades predichas por ambos modelos en un conjunto de categorías de riesgo y construir con las categorías del modelo nuevo y viejo dos tablas de contingencia, una para los eventos y otra para los no eventos. La elección de los puntos de corte para crear las categorías debe hacerse con sentido clínico.

Para el ejemplo anterior, si se crearan 3 categorías: “riesgo bajo”, con probabilidad predicha de 0 a 0,2; “riesgo intermedio”, con probabilidad mayor que 0,2 a 0,7 y “riesgo alto” con probabilidad mayor que 0,7 a 1, un programa que lo genera es

RECODE
  PVIEJA PNUEVA
  (0 thru 0.2=0)  (0.201 thru 0.5=1)  (0.501 thru 1=2)  INTO  CAT_VIEJO
  CAT_NUEVO.
EXECUTE .

VALUE LABELS CAT_VIEJO CAT_NUEVO 0 "Bajo" 1 "Medio" 2 "Alto".
EXECUTE.

* Crea, a partir de PVIEJA y PNUEVA, las categorías en las variables CAT_VIEJO Y CAT_NUEVO, con sus etiquetas.

CROSSTABS
  /TABLES=CAT_VIEJO  BY CAT_NUEVO  BY EVENTO
  /FORMAT= AVALUE TABLES
  /CELLS= COUNT
  /COUNT ROUND CELL.

Que construye la tabla

El NRI se define como la diferencia de las proporciones de sujetos con evento que suben de categoría y los que bajan, menos esa misma diferencia en los sujetos sin evento:

Es decir el NRI cuantifica lo que mejora la clasificación para los eventos, descontando lo que empeora para los no eventos. En el ejemplo las celdas en amarillo corresponden a subida de categoría, es decir mejoría del modelo para los eventos y empeoramiento para los no eventos y las celdas en verde bajada de categoría. Por tanto

Que informa de una mejoría neta en la clasificación del 3,8%.

Asumiendo independencia entre eventos y no eventos y sus probabilidades predichas, se puede calcular una prueba asintótica de la hipótesis nula de NRI=0, con una generalización de la prueba de McNemar para la comparación de proporciones no independientes.


 

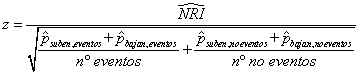
Que puede fácilmente implementarse en una hoja Excel. En el apartado de software de esta página puede descargarse una.

Referencias

    1.    Pencina MJ, D'Agostino RB, Sr., D'Agostino RB, Jr., Vasan RS. Evaluating the added predictive ability of a new marker: from area under the ROC curve to reclassification and beyond. Statistics in Medicine 2008; 27:157-172.