Modelo II o de efectos aleatorios

En este modelo se asume que las k muestras son muestras aleatorias de k situaciones distintas y aleatorias. De modo que un valor aislado Y_ij se puede escribir como:

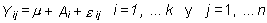
donde m es la media global, e_ij son variables (una para cada muestra) distribuidas normalmente, con media 0 y varianza s² (como en el modelo I) y A_i es una variable distribuida normalmente, independiente de las e_ij, con media 0 y varianza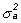

La diferencia con respecto al modelo I es que en lugar de los efectos fijos a_i ahora se consideran efectos aleatorios A_i.

Igual que en el modelo I se encuentra que MSE no se modifica en la H₁ y que al valor esperado de MSA se le añade el término de componente añadida (que aquí es una verdadera varianza ya que A_i es una variable aleatoria):

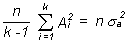
Para llegar a este resultado se utiliza la asunción de independencia entre A_i y e_ij y es, por tanto, muy importante en el modelo y conviene verificar si es correcta en cada caso. En el ejemplo de las cobayas significaría que las variaciones de grasa en el hígado de cada cobaya son independientes de las variaciones entre cobayas. Esta asunción se violaría si, por ejemplo, en el animalario existieran 2 cepas genéticas tales que en una de ellas la concentración de grasa en las células hepáticas fuera mayor y más variable que en la otra.

Por tanto, en H₀ tanto MSA como MSE estiman s², mientras que en H₁, MSE sigue estimando s² y MSA estima 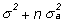. La existencia de esta componente añadida se contrasta con F= MSA/MSE y en caso afirmativo, la varianza de A_i se estima como:
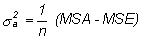