Pruebas para la homocedasticidad
Para que este contraste de hipótesis, basado en la F, lo sea de la igualdad de medias es necesario que todas las muestras provengan de una población con la misma varianza (s2), de la que MSE y MSA son estimadores. Por lo tanto es necesario comprobarlo antes de realizar el contraste. Del mismo modo que no se puede usar repetidamente la prueba basada en la en la t para comparar más de dos medias, tampoco se puede usar la prueba basada en la F para comparar más de dos varianzas. La prueba más usada para contrastar si varias muestras son homocedásticas (tiene la misma varianza) es la prueba de Bartlett.
La prueba se basa en
que, en la hipótesis nula de igualdad de
varianzas y poblaciones normales, un estadístico calculado a partir de las
varianzas muestrales y MSE sigue una
distribución Otras pruebas para
contrastar la homocedasticidad de varias muestras son la de Cochran y la de la F del cociente máximo, ambas similares y
de cálculo más sencillo pero restringidas al caso de iguales tamaños
muestrales. La de Cochran es particularmente útil para detectar si una varianza
es mucho mayor que las otras En el caso de que las
muestras no sean homocedásticas, no se puede, en principio, realizar el
análisis de la varianza. Existen, sin embargo,
soluciones alternativas: Sokal y Rohlf describen una prueba aproximada, basada
en unas modificaciones de las fórmulas originales. Hay situaciones en que
la heterocedasticidad es debida a falta de normalidad. En estos casos existen
transformaciones de los datos que estabilizan la varianza: la raíz cuadrada en
el caso de Poisson, el arco seno de la raíz cuadrada de p para la binomial, el logaritmo cuando la desviación estándar es
proporcional a la media. En la práctica, si las
pruebas de homocedasticidad obligan a rechazar la hipótesis nula, se prueba si con
alguna de estas transformaciones los datos son homocedásticos, en cuyo caso se
realiza el anova con los datos transformados. Hay que tener en cuenta que
estas pruebas van "al reves"de lo habitual. La hipótesis nula es lo
que se quiere probar, en consecuencia hay que usarlas con precaución. 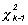
|
|
|
