Las estrategias de modelización son exactamente las mismas que las utilizadas en los otros modelos de regresión, contrastándose también del mismo modo la interacción y la confusión y pudiéndose usar también las variables dummy.

Ejemplo 9

Comparar la supervivencia de los tratamientos del ejemplo 5 controlando los posibles efectos de confusión e interacción de la edad.

En el ejemplo 5 se encontró que la supervivencia con ambos tratamientos ajustaba a un modelo exponencial, es decir con ambos tratamientos el riesgo es constante (por lo tanto se cumple la asunción de riesgo proporcional): 0,048 para el tratamiento 1 y 0,089 para el tratamiento 2, siendo ambos riesgos significativamente distintos.

Analizado con la regresión de Cox univariante

Se encuentra un resultado prácticamente superponible: hay una diferencia estadísticamente significativa (p=0.000) y el riesgo relativo es 1,892.

Sin embargo la edad media en ambos grupos es muy distinta (39,8 en los pacientes que reciben el tratamiento 1 y 64,7 en los que reciben el tratamiento 2) por lo tanto podría ser una variable de confusión.

Realizando un análisis multivariante, incluyendo en el modelo máximo: tratamiento, edad y el producto “tratamiento por edad” para evaluar la interacción y usando la estrategia hacia atrás

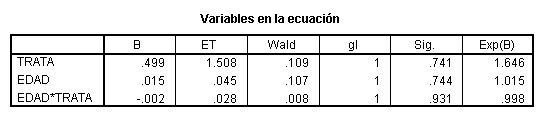
El modelo globalmente es significativo, evaluado con la prueba del logaritmo del cociente de verosimilitudes, que el SPSS denomina “prueba ómnibus”. El coeficiente del termino de interacción no es distinto de 0 (p=0,931) por lo tanto no se rechaza la hipótesis nula de no existencia de interacción y se elimina esa variable

Obsérvese que la variable EDAD es una variable de confusión: el riesgo relativo ha disminuido desde 1,892 estimado con el modelo simple a 1,449, Además ha dejado de ser significativo.

En consecuencia este sería el modelo final y la conclusión del análisis es que, una vez controlado por la edad, no hay diferencia significativa entre ambos tratamientos.