Modelo de regresión logística simple

Para una única variable independiente X, el modelo de regresión logística toma la forma:

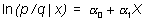
o, para simplificar la notación, simplemente:

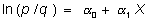
donde ln significa logaritmo neperiano, a₀ y a₁ son constantes y X una variable que puede ser aleatoria o no, continua o discreta. Este modelo se puede fácilmente generalizar para k variables independientes:

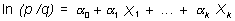
Por simplicidad, vamos a empezar por el modelo simple, extendiéndonos después al modelo múltiple.

Hay varias razones para plantear el modelo con el logaritmo del odds, en lugar de plantearlo simplemente con la probabilidad de éxito o con el odds. En primer lugar, el campo de variación de ln(p/q) es todo el campo real (de -¥ a ¥ ), mientras que, para p el campo es sólo de 0 a 1 y para p/q de 0 a ¥. Por lo tanto, con el modelo logístico no hay que poner restricciones a los coeficientes que complicarían su estimación. Por otro lado, y más importante, en el modelo logístico los coeficientes son, como veremos enseguida, fácilmente interpretables en términos de independencia o asociación entre las variables.

Hay otras formas equivalentes de poner el modelo, de modo que en diferentes textos se puede ver de otra forma, que para ciertas aplicaciones son más cómodas de usar:

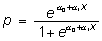
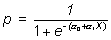
Estas dos últimas expresiones, si son conocidos los coeficientes, permiten calcular directamente la probabilidad del proceso binomial para los distintos valores de la variable X.

A la función:

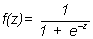
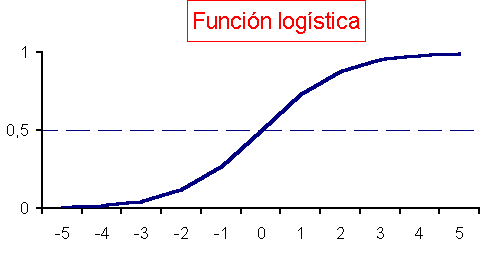
que aparece en otros muchos campos de la matemática aplicada, y cuya gráfica se muestra en la figura, se le denomina función logística. El modelo de regresión logística, por tanto, modeliza la probabilidad de un proceso binomial como la función logística de una combinación lineal de la(s) variable(s) dependiente(s).

Veamos, ahora, qué significan los coeficientes en el modelo. Supóngase por el momento que la variable X sólo puede tomar los valores 0 y 1. Para el valor X=0 el modelo queda:

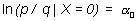
por tanto a₀ es el logaritmo del odds cuando la variable independiente es cero.

Para el valor X=1:

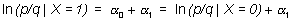
por lo tanto:

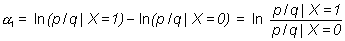
es decir a₁ es el logaritmo del cociente de los odds para los dos valores de la variable X, u "odds ratio" (OR), Si la variable binomial es independiente de la variable X, ambos odds son iguales, por lo tanto el odds ratio es 1 y su logaritmo será cero. Por lo tanto, para estudiar con un modelo logístico la independencia de las variables, basta con estudiar si el coeficiente a₁ es cero.

En el caso que se está considerando de una variable independiente con sólo dos valores, el riesgo relativo se puede poner, usando las otras formas del modelo:

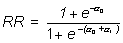
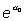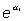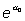Otro modo de expresar estos resultados es decir que es el odds cuando X=0 y el odds ratio entre X=1 y X=0. Si la variable X puede tomar más valores, evidentemente sigue siendo el odds cuando X=0 y 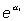el odds ratio para el aumento de una unidad en la variable X. Nótese que, por lo tanto, el modelo implica que este odds ratio es constante. Del mismo modo que en regresión lineal, cuando no tiene sentido físico X=0 (por ejemplo edad, presión arterial), 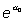se interpreta como el odds basal, es decir, el odds que no depende de la variable independiente.

Ejemplo 3: Se trata de estudiar el efecto dosis-respuesta para un tratamiento. A una muestra aleatoria de enfermos se la divide también aleatoriamente en 4 grupos, al primero no se le administra tratamiento, al segundo se le administra una cierta dosis, digamos 50 mg, al tercero 100 mg y al cuarto 150 mg y, como en el ejemplo anterior, se mide la respuesta como curación o no curación. Ahora la variable X tiene 4 valores que pueden ser, bien los mg de cada dosis (0, 50, 100, 150) o bien un código arbitrario para cada dosis (p.e. 0, 1, 2, 3). Si se plantea un modelo logístico, a₀ será el logaritmo del odds de la dosis 0 (el logaritmo del odds de la curación para los enfermos no tratados) y a₁ el logaritmo del odds ratio por aumento de unidad de dosis. Conviene tener presente dos aspectos: 1º la dependencia de a₁ de la codificación de la variable X, si se usan los mg la unidad es 1 mg y si se usan los códigos, la unidad es el cambio de dosis y 2º el modelo asume que el cambio en el logaritmo del odds es constante, es decir el logaritmo del odds cambia a ₁ por pasar de la dosis 0 a la 1, o por pasar de la dosis 2 a la 3. ¿Cuánto cambia por pasar de la dosis 0 a la 2?. Según el modelo:

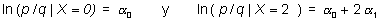
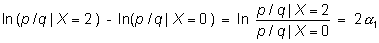
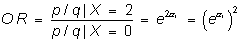
es decir, el cambio en el logaritmo del odds o, lo que es lo mismo, el logaritmo del odds ratio de la dosis 2 con respecto al no tratamiento es 2 veces el logaritmo del odds ratio de la dosis 1, por consiguiente el odds ratio de la dosis 2 es el cuadrado del odds ratio de la dosis 1, o dicho de otro modo, el modelo asume efectos multiplicativos. (ésta es la única asunción del modelo). En general, para un aumento de la variable X desde x₀ a x₁, siendo d = x₀ - x₁

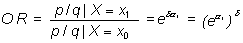
Ejemplo 4: Para estudiar la posible asociación entre la tuberculosis pulmonar y el contacto con el ganado vacuno se eligen aleatoriamente 100 enfermos y, también aleatoriamente, 100 personas no enfermas y se investiga en ambos grupos dicho contacto. Obsérvese que el diseño del estudio es diferente al de los ejemplos anteriores (ahora es un estudio caso-control), ahora se extraen dos muestras de dos poblaciones diferentes (enfermos y no enfermos). El resultado del estudio puede presentarse también en forma de tabla de doble entrada similar a la del ejemplo 1:

A partir de esta tabla no se pueden estimar p|X=0 ni p|X=1 ya que los datos para X=0 y X=1 no provienen de una única muestra. Dado que se ha muestreado independientemente en enfermos y no enfermos, las probabilidades que sí se pueden estimar a partir de la tabla son p(X=0|E), p(X=0|nE), p(X=1|E) y p(X=1|nE) cuyos estimadores son respectivamente A/(A+B), C/(C+D), B/(A+B) y D/(C+D).

Para calcular a partir de ellos p(E|X=0), p(nE|X=0), p(E|X=1) y p(nE|X=1), aplicando el teorema de Bayes, sería necesario conocer p(E) y p(nE), para las que la tabla no ofrece ningún estimador, por consiguiente no se puede estimar el odds para X=0 ni para X=1. Sí se puede, sin embargo, (aplicando el teorema de Bayes) estimar el odds ratio y se obtiene:

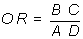
Obsérvese que, como en el ejemplo anterior, es también el cociente de los productos cruzados de los elementos de la tabla.

Es decir, con el esquema de muestreo de este ejemplo se puede estimar el odds ratio, pero no el odds para X=0, o dicho en términos del modelo logístico, se puede estimar a₁, pero no a₀. Sin embargo, el estimador de a₁ es el mismo que en los ejemplos anteriores que corresponden a un único proceso de muestreo o al muestreo de los estudios de cohorte. Dicho de otro modo, cuando se aplica el modelo logístico a estudios caso-control, el coeficiente a₀ no tiene ningún significado, sin embargo el coeficiente a₁ significa lo mismo (y se estima del mismo modo) que en estudios de cohortes.