MODELOS DE REGRESION LOGISTICA

V. Abraira

Bibliografía:

V. Abraira, A.Pérez de Vargas
Métodos Multivariantes en Bioestadística.
Ed. Centro de Estudios Ramón Areces. 1996.

L.C. Silva Ayçaguer
Excursión a la regresión logística en Ciencias de la Salud
Díaz de Santos. 1995

D.W. Hosmer, S. Lemeshow
Applied Logistic Regression.
John Wiley & Sons. 1989.

Asociación entre variables binomiales

Se dice que un proceso es binomial cuando sólo tiene dos posibles resultados: "éxito" y "fracaso", siendo la probabilidad de cada uno de ellos constante en una serie de repeticiones. A la variable número de éxitos en n repeticiones se le denomina variable binomial. A la variable resultado de un sólo ensayo y, por tanto, con sólo dos valores: 0 para fracaso y 1 para éxito, se le denomina binomial puntual.

Un proceso binomial está caracterizado por la probabilidad de éxito, representada por p (es el único parámetro de su función de probabilidad), la probabilidad de fracaso se representa por q y, evidentemente, ambas probabilidades están relacionadas por p+q=1. En ocasiones, se usa el cociente p/q, denominado "odds", y que indica cuánto más probable es el éxito que el fracaso, como parámetro característico de la distribución binomial aunque, evidentemente, ambas representaciones son totalmente equivalentes.

Los modelos de regresión logística son modelos de regresión que permiten estudiar si una variable binomial depende, o no, de otra u otras variables (no necesariamente binomiales): Si una variable binomial de parámetro p es independiente de otra variable X, se cumple p=p|X, por consiguiente, un modelo de regresión es una función de p en X que a través del coeficiente de X permite investigar la relación anterior.

Ejemplo 1: Se quiere comparar la eficacia de dos tratamientos alternativos para una misma enfermedad. Asumiendo que el proceso "curar" sólo tiene dos resultados: sí o no y que la probabilidad de curación es la misma para todos los enfermos, se trata de un proceso binomial. Se trata de ver si este proceso está asociado, o no, con el tratamiento, es decir, si la probabilidad de curación dado el tratamiento A es igual, o distinta, a la probabilidad de curación dado el tratamiento B. Supóngase que sobre una muestra aleatoria de 40 enfermos, dividida aleatoriamente en dos grupos de 20, a cada uno de los cuales se le suministra un tratamiento, se obtienen los siguientes resultados:

Si se define la variable tratamiento como X=1 para el tratamiento A y X=0 para el B, a partir de la tabla podemos estimar la probabilidad de curación para el tratamiento B: p|(X=0)=13/20 y para el tratamiento A: p|(X=1)=18/20 Como ambas probabilidades son distintas, "parece" que la probabilidad de curación depende del tratamiento. Las preguntas son: ¿esta dependencia es generalizable ("estadísticamente significativa")? ¿cuánto depende ("clínicamente relevante")?

La primera pregunta la podemos resolver mediante la prueba c², la segunda mediante las denominadas "medidas de asociación", o "de fuerza de la asociación", o "de efecto": diferencia de riesgo (DR), riesgo relativo (RR) y "odds ratio" (OR). En el ejemplo:

DR: 18/20 - 13/20 = 5/20 =0,25

RR: (18/20)/(13/20) = 18/13 = 1,38

OR: ((18/20)/(2/20))/(13/20)/(7/20) =(18x7)/(13x2) = 4,85

DR es 0 en caso de no diferencia, mientras que RR y OR son ambos 1. Recordemos que el OR, aunque es la medida menos intuitiva^1,2, es la más extendida por diversas razones y que es conveniente que a estas estimaciones puntuales las acompañemos de su intervalo de confianza que nos indica la precisión de la estimación.

Ejemplo 2: Para refrescar los conceptos de odds ratio y riesgo relativo. Sean dos juegos, en uno (X=0) se apuesta sobre la salida de una cierta cara en una tirada de un dado, y en otro (X=1) sobre la salida de una cara en la tirada de una moneda. Evidentemente, la probabilidad de ganar es para el dado p|(X=0)=1/6 y para la moneda p|(X=1)=1/2 El riesgo relativo es:

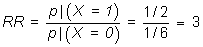
que, como es distinto de 1, quiere decir que la probabilidad de ganar está asociada al tipo de juego, y que es 3 veces más probable ganar con la moneda que con el dado. El odds ratio para este ejemplo es:

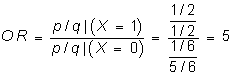
el odds para la moneda es 5 veces el odds del dado, es decir, a la larga la razón de partidas ganadas/perdidas es 5 veces mayor para la moneda que para el dado. Para decidir a que juego interesa jugar hay que comparar este odds ratio con la razón de los cocientes entre lo que se puede ganar y perder en cada jugada en ambos juegos. El OR está siempre más alejado de 1 que el RR, aunque cuando las probabilidades son muy pequeñas la diferencia (entre el OR y el RR) es pequeña.

Se trata, ahora, de comparar el juego de la lotería nacional (X=1) en el que el premio es para un número extraído de entre 100.000, con el de la lotería primitiva (X=0) en que se premia una combinación de 6 números de entre las que se pueden formar con 49 números. Resulta p|(X=1)=1/100.000. El número de combinaciones de 6 números que se pueden formar con 49 es C_49;6=13.983.816 por lo tanto p|(X=0)=1/13.983.816 y:

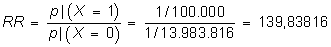
es aproximadamente 140 veces más probable ganar en el juego de la lotería que en el de la lotería primitiva. El odds ratio para este ejemplo es:

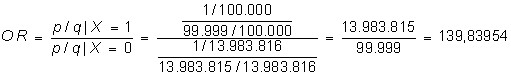
que, como era de esperar, debido a los pequeños valores de p|X=1 y p|X=0 es prácticamente igual que el riesgo relativo (recordar cuando la prevalencia es baja, el OR estima el RR).

Otras lecturas recomendadas

Odds ratios should be avoided when events are common. Altman DG et al. BMJ. 317:1318. 1998

When can odds ratios mislead? Davies HTO et al. BMJ. 316:989-991. 1998

Medidas del efecto de un tratamiento (I): reducción absoluta del riesgo, reducción relativa del riesgo y riesgo relativo. Abraira V. SEMERGEN 26: 535-536. 2000.

Medidas del efecto de un tratamiento (II): odds ratio y número necesario para tratar. Abraira V. SEMERGEN 27: 418-420. 2001.