Modelo de regresión lineal múltiple

Las variables biológicas suelen presentar multicorrelaciones. P.e. para estudiar el efecto del consumo de grasas saturadas en el nivel del colesterol en sangre, se puede plantear un modelo de RLS, sin embargo el nivel de colesterol puede depender también de otras variables: consumo de otras substancias, ejercicio realizado, edad, factores metabólicos genéticos, etc.

Si, para cada valor del consumo de grasas, las demás variables se distribuyen aleatoriamente, la estimación por RLS es adecuada y la variación "debida" a las otras variables estaría incluida en la variación aleatoria alrededor de la regresión, pero en caso contrario la estimación sería incorrecta, si p.e., las costumbres dietéticas variaran con la edad y ésta influyera en el colesterol, una parte no cuantificada de la variación del colesterol que el modelo atribuye al consumo de grasas sería "debida" a la edad.

La regresión lineal múltiple (RLM) es un modelo que permite estudiar estos efectos. El modelo es

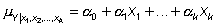
a₀: media de Y cuando todas las X_i son cero (cuando no tiene sentido X_i=0, p.e. edad, se interpreta como la media de Y que no depende de las X_i).
a_i: cambio en la media de Y cuando X_i aumenta una unidad permaneciendo constantes las demás.

Las asunciones del modelo son una generalización de las de RLS y dado el resultado de RLS no vamos a distinguir entre modelo I y II.

La estimación de los coeficientes también se hace por mínimos cuadrados o máxima verosimilitud y se obtienen los mismos resultados. Estos resultados, usando notación matricial, son (incluyen como caso particular la RLS):

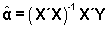
siendo 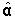la matriz columna de coeficientes estimados, Y la matriz columna de observaciones de la variable dependiente y X la denominada matriz de diseño

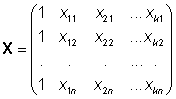
es decir la matriz de datos con una primera columna de 1's. Estos coeficientes se distribuyen como una normal multivariante cuya matriz de medias son los verdaderos coeficientes y matriz de varianzas-covarianzas

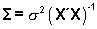
un buen estimador de s² es

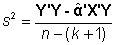
que se distribuye como una c² con n - (k+1) grados de libertad.

Estas fórmulas ponen de manifiesto unas limitaciones al resolver estos modelos. Para ello hay que invertir una matriz y no todas las matrices pueden invertirse (singulares). En dos situaciones no se puede: