El problema de la colinealidad
Es uno de los problemas más desesperantes con que uno se puede encontrar en un análisis de regresión. Como ya vimos al hablar de la estimación de los coeficientes, si en un modelo de RLM alguna variable independiente es combinación lineal de otras, el modelo es irresoluble, debido a que, en ese caso, la matriz X'X es singular, es decir, su determinante es cero y no se puede invertir.
A este fenómeno se le denomina colinealidad. Que una variable X1 sea combinación lineal de otra X2, significa que ambas están relacionadas por la expresión X1 = b1 + b2X2, siendo b1 y b2 constantes, por lo tanto el coeficiente de correlación entre ambas variables será 1.
Del mismo modo, que una variable X1 sea combinación lineal de otras X2, ..., Xi con i>2, significa que dichas variables están relacionadas por la expresión X1 = b1 > + b2 X2 + ... + bi Xi, siendo b1,..., bi constantes y por tanto, el coeficiente de correlación múltiple RX1|X2,...Xi también será 1.
Otro modo, por tanto, de definir la colinealidad es decir que existe colinealidad cuando alguno de los coeficientes de correlación simple o múltiple entre algunas de las variables independientes es 1, es decir, cuando algunas variables independientes están correlacionadas entre sí.
En la práctica, esta colinealidad exacta raras veces ocurre, pero sí surge con cierta frecuencia la llamada casi-colinealidad, o por extensión, simplemente colinealidad en que alguna variable es "casi" combinación lineal de otra u otras, o dicho de otro modo, algunos coeficientes de correlación simple o múltiple entre las variables independientes están cercanos a 1, aunque no llegan a dicho valor.
En este caso la matriz X'X es casi-singular, es decir su determinante no es cero pero es muy pequeño. Como para invertir una matriz hay que dividir por su determinante, en esta situación surgen problemas de precisión en la estimación de los coeficientes, ya que los algoritmos de inversión de matrices pierden precisión al tener que dividir por un número muy pequeño, siendo además inestables.
Además, como la matriz de varianzas de los estimadores es proporcional a X'X, resulta que en presencia de colinealidad los errores estándar de los coeficientes son grandes (hay imprecisión también en sentido estadístico).
Por consiguiente, a la hora de plantear modelos de RLM conviene estudiar previamente la existencia de casi-colinealidad (la colinealidad exacta no es necesario estudiarla previamente, ya que todos los algoritmos la detectan, de hecho no pueden acabar la estimación). Como medida de la misma hay varios estadísticos propuestos, los más sencillos son los coeficientes de determinación de cada variable independiente con todas las demás, es decir
![]()
y, relacionados con ellos, el factor de inflación de la varianza (FIV) y la tolerancia (T), definidos como
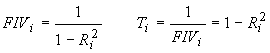
Una regla empírica, citada por Kleinbaum, consiste en considerar que existen problemas de colinealidad si algún FIV es superior a 10, que corresponde a algún R2i 0,9 y Ti < 0,1.
Aunque puede existir colinealidad con FIV bajos, además puede haber colinealidades que no impliquen a todas las variables independientes y que, por tanto, no son bien detectadas por el FIV.
Otra manera, más completa, de detectar colinealidad es realizar un análisis de componentes principales de las variables independientes. Esta técnica es matemáticamente compleja y aquí se hace sólo un resumen de la misma necesario para entender el diagnóstico de la colinealidad.
Se denominan componentes principales de un conjunto de variables a otras variables, combinación lineal de las originales y que tienen tres propiedades características:
i) son mutuamente independientes (no están correlacionadas entre sí).
ii) mantienen la misma información que las variables originales.
iii) tienen la máxima varianza posible con las limitaciones anteriores.
De hecho, para modelos predictivos los componentes principales son las variables independientes ideales.
La varianza de cada componente principal es un autovalor (número asociado a una matriz) de la matriz de varianzas-covarianzas de las variables originales.
El número de autovalores nulos indica el número de variables que son combinación lineal de otras (el número de colinealidades exactas) y autovalores próximos a cero indican problemas graves de colinealidad.
El cálculo de los autovalores permite, por lo tanto, determinar no sólo la existencia de colinealidad, sino también el número de colinealidades.
Para determinar cuándo un autovalor pequeño está suficientemente próximo a cero se usa su valor relativo con respecto al mayor, en este sentido, para cada autovalor se define el índice de condición como la raíz cuadrada del cociente entre el mayor de ellos y dicho autovalor y se denomina número de condición al mayor de los índices de condición.
Para Belsley índices de condición entre 5 y 10 están asociados con una colinealidad débil, mientras que índices de condición entre 30 y 100 señalan una colinealidad moderada a fuerte.
Una vez determinada la presencia y el número de colinealidades, es conveniente averiguar qué variables están implicadas en ellas. Usando ciertas propiedades de la matrices se puede calcular la proporción de la varianza de las variables sobre cada componente.
Si dos o más variables tienen una proporción de varianza alta en un componente indica que esas variables están implicadas en la colinealidad y, por tanto, la estimación de sus coeficientes está degradada por la misma.
Belsley propone usar conjuntamente los índices de condición y la proporción de descomposición de varianza para realizar el diagnóstico de colinealidad, usando como umbral de proporción alta 0,5 de modo que, finalmente, dicho diagnóstico se hará:
Los índices de condición altos (mayores que 30) indican el número de colinealidades y la magnitud de los mismos mide su importancia relativa.
Si un componente tiene un índice de condición mayor que 30 y dos o más variables tienen un proporción de varianza alta en el mismo, esas variables son colineales.
Como ya se indicó más arriba, la mejor solución a los problemas de colinealidad consiste en plantear el modelo de regresión con los componentes principales en lugar de con las variables originales, si bien esta solución sólo está indicada en los modelos predictivos.
En los modelos estimativos no tiene sentido, ya que el interés del modelo es, justamente, estimar el efecto sobre la variable independiente de una variable determinada y no interesa, por lo tanto, usar otras variables distintas.
Otras soluciones alternativas planteables en ambos tipos de modelos pueden ser: cambios de escala en las variables, incluyendo el centrado de las mismas (restar a cada variable su media) o, incluso, eliminar alguna de las variables colineales.
En este mismo sentido hay que tener en cuenta que las variables producto introducidas para estudiar la interacción pueden dan lugar a problemas de colinealidad y no se recomienda, por lo tanto, que un modelo contenga muchos términos de interacción.
Si una variable toma el mismo valor para todas las observaciones (tiene varianza cero) existe colinealidad exacta con el término independiente, y si una variable tiene varianza casi cero (toma valores muy próximos para todas las observaciones) existe casi-colinealidad.
Puede ocurrir que una varianza pequeña sea debida a una escala inapropiada para la variable, por ejemplo, si la edad de sujetos adultos se mide en décadas se obtiene una varianza 100 veces menor que si se midiera en años. En este caso un cambio de escala puede evitar el problema de la colinealidad.
También se puede perder precisión en el cálculo de (X'X)-1 por la existencia de variables con varianzas excesivamente grandes, en cuyo caso el cambio de escala aconsejable sería el contrario, por ejemplo, podría dar lugar a problemas de precisión medir la edad en días.
Ejemplo 10
Realizar el estudio de colinealidad en los datos del ejemplo 5, usando los FIV, los índices de condición y la matriz de proporción de descomposición de la varianza de los estimadores.
Realizando los análisis de regresión de cada una de las variables independientes con todas las demás, se obtienen los siguientes coeficientes de determinación, tolerancia y factores de inflación de la varianza
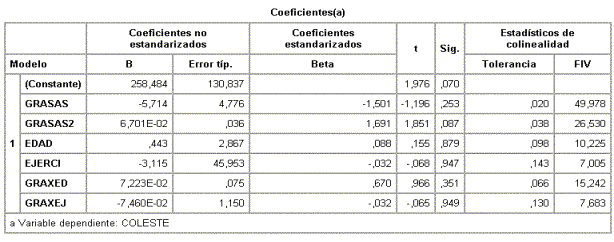
que indican problemas graves de colinealidad.
Obsérvese que el factor de inflación mayor corresponde a la variable GRASAS, resultado esperable debido a que se han creado tres variables más (GRASA2, GRAXED y GRAXEJ) a partir de ella.
Los autovalores de la matriz X'X y los índices de condición, así como la matriz de proporción de descomposición de varianza son:
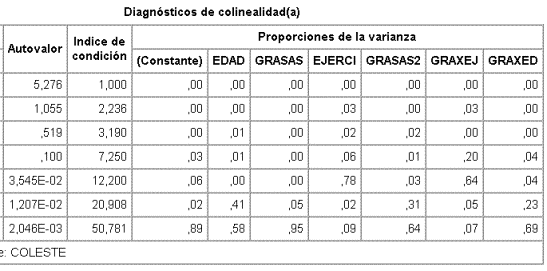
Hay un índice de condición alto (50,781) y asociado con el mismo hay cinco variables (el término constante, GRASAS, GRASA2, EDAD y GRAXED) con proporción de varianza alta.
Nos indica, por tanto, que GRASAS es colineal con GRASA2, GRAXED (no nos sorprende), EDAD y con la constante.
Al existir esta última colinealidad, el centrado de variables podría mejorar el problema, se podría también renunciar a estudiar los términos no lineales GRASA2 y GRAXED.
Empecemos por centrar las variables continuas.
GRASAC
= GRASAS - 39,7
EDADC = EDAD - 36,25
GRASC2 = GRASAC x GRASAC
GRXEDC = GRASAC x EDADC
GRXEJC = GRASAC x EJERC
y, para ellas, el diagnóstico de colinealidad queda:
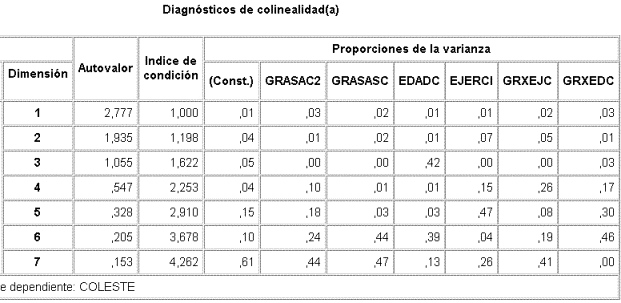
y tanto los índices de condición como la proporción de varianza, indican que el centrado ha resuelto los problemas de colinealidad.
Referencias
D.G. Kleinbaum, L.L. Kupper,
K.E. Muller
Applied Regression Analysis and
Other Multivariables Methods.
PWS-KENT Publishing Company. 1988.
D.A. Belsley
Conditioning Diagnostics: Collinearity and Weak Data in Regression.
John Wiley &Sons. 1991
|
|

|

|
|
