Estrategias de modelización

El problema es ¿cómo usamos todo esto?. Debido a los dos objetivos distintos que un análisis de regresión puede tener es difícil establecer una estrategia general para encontrar el mejor modelo de regresión, es más, el mejor modelo significa cosas distintas con cada objetivo.

En un análisis predictivo el mejor modelo es el que produce predicciones más fiables para una nueva observación, mientras que en un análisis estimativo el mejor modelo es el que produce estimaciones más precisas para el coeficiente de la variable de interés.

En ambos casos se prefiere el modelo más sencillo posible (a este modo de seleccionar modelos se le denomina parsimonia), de modo que en un análisis estimativo, se puede excluir del modelo una variable que tenga un coeficiente significativamente distinto de cero y que su contribución a la predicción de la variable dependiente sea importante, porque no sea variable de confusión para la variable de interés (el coeficiente de dicha variable no cambia), en un análisis predictivo esa variable no se excluiría.

Sin embargo, hay una serie de pasos que deben realizarse siempre:
i) Especificación del modelo máximo.
ii) Especificación de un criterio de comparación de modelos y definición de una estrategia para realizarla.
iii) Evaluación de la fiabilidad del modelo.

i) Especificación del modelo máximo

Se trata de establecer todas las variables que van a ser consideradas. Recuérdese que el modelo saturado (el máximo que se puede considerar) tiene n - 1 variables pero que, con este modelo, los grados de libertad para SSE son cero, y R²=1, de modo que, en general, el modelo saturado no tiene interés y el modelo máximo deberá tener menos variables independientes que el modelo saturado (un criterio habitual es incluir como máximo una variable cada 10 casos).

El criterio para decidir qué variables forman el modelo máximo lo establece el investigador en función de sus objetivos y del conocimiento teórico que tenga sobre el problema, evidentemente cuanto menor sea el conocimiento previo mayor tenderá a ser el modelo máximo.

Un modelo máximo grande minimiza la probabilidad de error tipo II o infraajuste, que en un análisis de regresión consiste en no considerar una variable que realmente tiene un coeficiente de regresión distinto de cero.

Un modelo máximo pequeño minimiza la probabilidad de error tipo I o sobreajuste (incluir en el modelo una variable independiente cuyo coeficiente de regresión realmente sea cero).

Debe tenerse en cuenta también que un sobreajuste, en general, no introduce sesgos en la estimación de los coeficientes (los coeficientes de las otras variables no cambian), mientras que un infraajuste puede producirlos, pero que un modelo máximo grande aumenta la probabilidad de problemas de colinealidad.

En el modelo máximo deben considerarse también los términos de interacción que se van a introducir (en un modelo estimativo sólo interesan interacciones entre la variable de interés y las otras) y la posibilidad de incluir términos no lineales. En Biología son muy frecuentes relaciones no lineales, que pueden modelizarse con términos cuadráticos o de mayor orden o con transformaciones tales como la exponencial o el logaritmo.

En el ejemplo 5 podría considerarse que la dependencia del nivel de colesterol en sangre con las grasas consumidas puede no ser lineal y presentar, por ejemplo, saturación: por encima de un cierto nivel de grasas ingeridas el colesterol en sangre ya no sube más, o un punto umbral: las grasas consumidas elevan el colesterol, sólo si sobrepasan un cierto valor. Cada uno de estos fenómenos puede modelarse satisfactoriamente con un término cuadrático o una transformación logarítmica o exponencial (introducir en el modelo junto con, o en lugar de, la variable GRASAS, la variable (GRASAS)²; o log(GRASAS) o EXP(GRASAS)) y ambos juntos, con un término cúbico ((GRASAS)³).

ii) Comparación de modelos

Debe establecerse cómo y con qué se comparan los modelos. Si bien hay varios estadísticos sugeridos para comparar modelos, el más frecuentemente usado es la F parcial, recordando que cuando los dos modelos sólo difieren en una variable, el contraste sobre la F parcial es exactamente el mismo que el realizado con la t sobre el coeficiente de regresión, pero a veces interesa contrastar varias variables conjuntamente mejor que una a una (por ejemplo todos los términos no lineales) o, incluso, es necesario hacerlo (por ejemplo para variables indicadoras).

Hay que hacer notar que en un análisis estimativo el criterio para incluir o excluir variables distintas a las de interés, es sobre todo los cambios en los coeficientes y no los cambios en la significación del modelo.

Los distintos modelos a comparar se pueden construir de dos formas: por eliminación o hacia atrás ("backward") y por inclusión o hacia adelante ("forward").

Con la primera estrategia, se ajusta el modelo máximo y se calcula la F parcial para cada variable como si fuera la última introducida (que es equivalente a la t para esa variable), se elige la menor de ellas y se contrasta con el nivel de significación elegido. Si es mayor o igual que el valor crítico se adopta este modelo como resultado del análisis y si es menor se elimina esa variable y se vuelve a repetir todo el proceso hasta que no se pueda eliminar ninguna variable.

Con la estrategia hacia adelante, se empieza con un modelo de una variable, aquella que presente el mayor coeficiente de correlación simple. Se calcula la F parcial para la inclusión de todas las demás, se elige la mayor de ellas y se contrasta con el nivel de significación elegido. Si es menor que el valor crítico, se para el proceso y se elige el modelo simple como mejor modelo, y si es mayor o igual que dicho valor crítico, esa variable se incluye en el modelo y se vuelve a calcular la F parcial para la inclusión de cada una de todas las restantes, y así sucesivamente hasta que no se pueda incluir ninguna más.

Una modificación de esta última estrategia es la denominada "stepwise" que consiste en que, cada vez que con el criterio anterior se incluye una variable, se calculan las F parciales de todas las incluidas hasta ese momento como si fueran las últimas y la variable con menor F parcial no significativa, si la hubiera, se elimina. Se vuelven a calcular las F parciales y se continua añadiendo y eliminando variables hasta que el modelo sea estable.

Las variaciones a estas estrategias consisten en que, con cualquiera de ellas, se puede contrastar varias variables en lugar de una sola y que, en aplicación del principio jerárquico, cuando se contrasta un término de interacción, el modelo debe incluir todos los términos de orden inferior y, si como resultado del contraste, dicho término permanece en el modelo, también ellos deben permanecer en el mismo, aunque no se pueda rechazar que los coeficientes correspondientes no son distintos de cero.

En cualquier caso, puede ser peligroso aplicar cualquiera de estas estrategias automáticamente (con un paquete estadístico, por ejemplo) por lo que se ha comentado más arriba sobre los distintos criterios dependiendo del objetivo del estudio, los términos de interacción y las variables indicadoras.

Ejemplo 9

Encontrar el mejor modelo para los datos del ejemplo 5 , con el objetivo de estimar el efecto del consumo de grasas sobre el nivel del colesterol y usando la estrategia hacia atrás.

El modelo máximo estaría formado por EDAD, GRASAS, EJERC (teniendo en cuenta que está codificado en 3 niveles podría ser conveniente analizarlo a través de 2 variables indicadoras, pero no se va a hacer por simplicidad del ejemplo), se considerará también el término (GRASAS)² para analizar relaciones no lineales y los términos de interacción entre GRASAS y EDAD y entre GRASAS y EJERC. La interacción entre EDAD y EJERC en este caso no interesa, puesto que la variable de interés es GRASAS.

En el archivo de datos, habrá que crear 3 variables nuevas: GRASA2 = (GRASAS)², GRAXED = GRASAS x EDAD y GRAXEJ = GRASAS x EJERC y el resultado del análisis del modelo máximo es

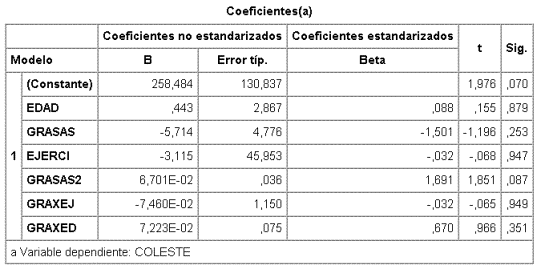
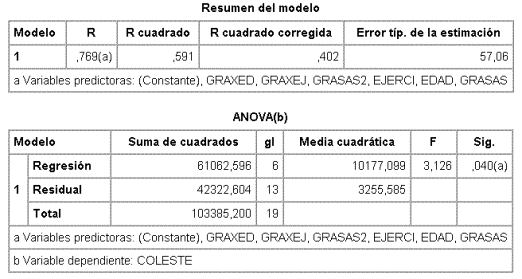
Recordando que la F parcial de una variable dadas todas las demás es el cuadrado del valor de t para el coeficiente de la misma, la variable que tiene menor F parcial no significativa es GRAXEJ, por lo tanto esta variable se elimina y se ajusta ahora un modelo excluyéndola.

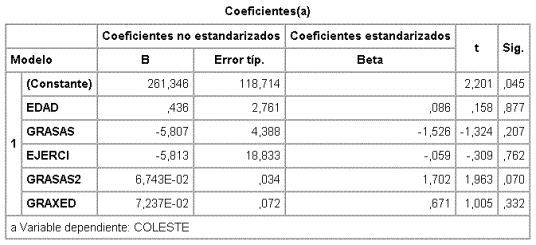
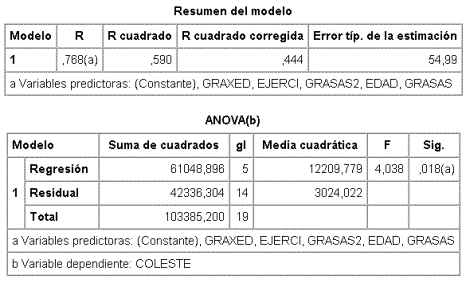
Obsérvese que R apenas ha disminuido (R siempre disminuye al quitar variables y su disminución es otro de los estadísticos propuestos para comparar modelos) pero la F global ha mejorado (p=0,018 frente a 0,040).

En este modelo la menor F parcial no significativa corresponde a EDAD, sin embargo, en el modelo todavía está el término de interacción entre EDAD y GRASAS (GRAXED) en consecuencia EDAD no se puede quitar (principio jerárquico), la siguiente F parcial corresponde a EJERCI y no es significativa, en consecuencia se quita EJERCI. El nuevo modelo es

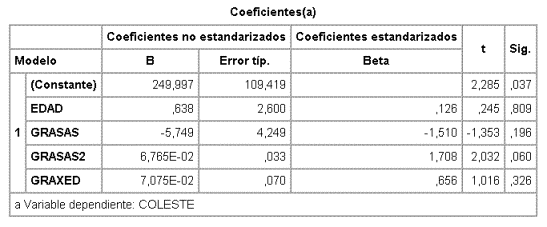
No hay cambios en los coeficientes de GRASAS, ni GRASA2, ni GRAXED (EJERCI no es variable de confusión, por lo tanto se puede eliminar definitivamente. Si hubiera habido cambios no se podría eliminar a pesar de no ser significativa).

La variable con menor F parcial sigue siendo EDAD y la siguiente GRAXED. Se quita y el nuevo modelo es

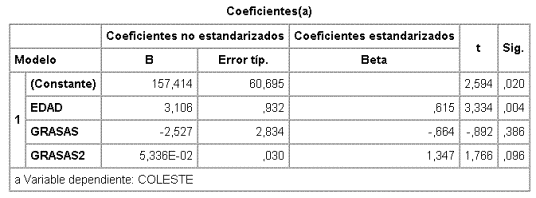
La menor F parcial no significativa es, ahora, la de GRASAS, pero GRASA2 debe contrastarse antes y como tampoco es significativa (obsérvese, no obstante, que está en el borde y podría tratarse de un problema de falta de potencia) se quitaría GRASA2. El modelo finalmente queda

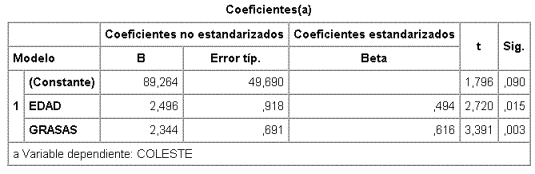
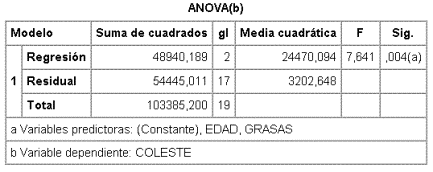
Donde la F global es significativa siendo también significativas las F parciales de las dos variables que permanecen, de modo que éste podría ser el modelo final.

No obstante, como el objetivo del estudio es estimar el efecto de las grasas, se debería probar un modelo sin la edad y si en éste último modelo no hubiera cambios en la estimación del efecto de las grasas, podría quitarse la edad, en aplicación del principio de parsimonia.

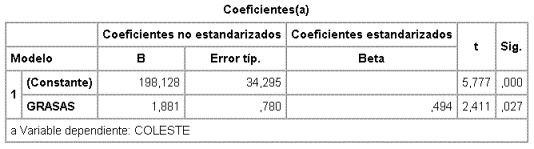
Como el cambio en el coeficiente es mayor que el 10%, concluimos que EDAD es variable de confusión y el modelo final es el que comntoene GRASAs y EDAD.

iii) Evaluación de la fiabilidad del modelo

Una vez encontrado el mejor modelo hay que evaluar su fiabilidad, es decir, evaluar si se comporta igual en otras muestras extraídas de la misma población. Evidentemente, el modo más completo de evaluarlo será repetir el estudio con otra muestra y comprobar que se obtienen los mismos resultados, aunque generalmente esta aproximación resulta excesivamente costosa.

Otra aproximación alternativa consiste en partir aleatoriamente la muestra en dos grupos y ajustar el modelo con cada uno de ellos y si se obtienen los mismos resultados se considera que el modelo es fiable. Esta aproximación es demasiado estricta ya que, en la práctica, casi nunca se obtienen los mismos resultados.

Una validación menos estricta consiste en ajustar el modelo sobre uno de los grupos (grupo de trabajo) y calcular su R², que se puede interpretar como el cuadrado del coeficiente de correlación simple entre la variable dependiente y las estimaciones obtenidas en la regresión.

Después, y con el modelo obtenido en el grupo de trabajo, calcular las estimaciones de la variable dependiente en el otro grupo (grupo de validación) y calcular el coeficiente de correlación simple al cuadrado entre estas estimaciones y la variable dependiente (R²*), a este coeficiente se le denomina coeficiente de correlación de validación cruzada. A la diferencia R²-R²* se le denomina reducción en la validación cruzada y, aunque no hay reglas firmes al respecto, se considera que una reducción superior a 0,90 indica un modelo no fiable y una reducción inferior a 0,10 indica un modelo muy fiable.

Otras lecturas

Silva Ayçaguer L.C., Barroso Utra I.M. Selección algorítmica de modelos en las aplicaciones biomédicas de la regresión múltiple. Medicina Clínica. 2001;116:741-745.