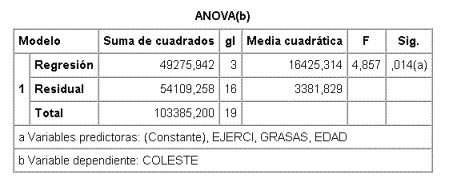
Análisis de la varianza de la regresión

De un modo similar a RLS se puede descomponer la variación de la variable Y de dos componentes: uno la variación de Y alrededor de los valores predichos por la regresión y otro con la variación de los valores predichos alrededor de la media. Si el modelo lineal no es adecuado, ambos estimadores estimarían la varianza de Y y si es adecuado no. Comparando ambos estimadores con la prueba de la F se contrasta lo adecuado del modelo. Para el ejemplo 5

Obsérvese que, a diferencia de la RLS, este contraste no es equivalente al realizado sobre los coeficientes.

Se define también el coeficiente de determinación como el cociente entre la suma de cuadrados de la regresión y la suma de cuadrados total (R² = SSR/SST) y a su raíz cuadrada (R) se le denomina coeficiente de correlación múltiple.

Además de esta prueba global del modelo basada en el análisis de la varianza, se pueden plantear pruebas parciales sobre si una variable, o un grupo de variables, añadidas a un modelo previo lo mejoran.

Se tiene un modelo

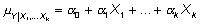
y se añade una nueva variable X*, con el primer modelo se tiene una SSR(Y,X₁,...,X_k) y con el nuevo otra SSR(Y,X₁,...,X_k,X*), la diferencia entre ambas será lo que ha mejorado la suma de cuadrados por añadir la variable X* y tendrá 1 grado de libertad.

SSR(Y,X*|X₁,...,X_k) = SSR(Y,X₁,...,X_k,X*) - SSR(Y,X₁,...,X_k) = SSE(Y,X₁,...,X_k) - SSE(Y,X₁,...,X_k,X*)

y el cociente

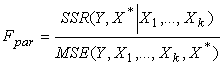
llamado F parcial, tendrá una distribución F con 1 y n-(k+2) grados de libertad en la hipótesis nula de que la nueva variable X* no mejore el modelo. Evidentemente este contraste es totalmente equivalente a contrastar que el coeficiente a* de la nueva variable es cero con la prueba basada en la t.

Del mismo modo, si al modelo original se le añaden p variables X₁*,...,X_p*, se puede definir

SSR(Y,X₁*,...,X_p*|X₁,...,X_k) = SSR(Y,X₁,...,X_k,X₁*,...,X_p*) - SSR(Y,X₁,...,X_k) = SSE(Y,X₁,...,X_k) - SSE(Y,X₁,...,X_k,X₁*,...,X_p*)

que tiene p grados de libertad, y el cociente

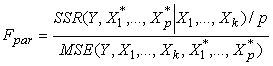
se distribuye como una F_p,n-(k+p+1) en la hipótesis nula de que las nuevas p variables X₁*, ..., X_p* no mejoren el modelo con respecto a las k variables originales y permite contrastar dicha hipótesis.

Ejemplo 6

Con los datos del ejemplo 5, realizar el contraste de la F parcial para añadir la variable ejercicio a un modelo que sólo contenga la edad y las grasas consumidas.

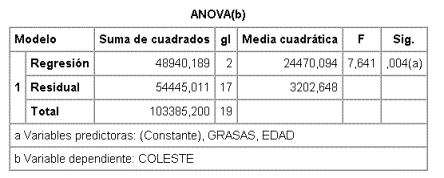
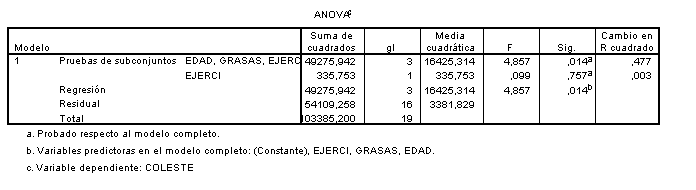
Por lo tanto, comparando esta tabla con la del modelo completo

SSR(COLEST,EJERC|GRASAS,EDAD) =
  SSR(COLEST,GRASAS,EDAD,EJERC) - SSR(COLEST,GRASAS,EDAD) = 49275,94 - 48940,18 = 335,76

por tanto F_par=335,76/3381,83=0,099

que se distribuye como una F_1,16. Como F_0,05(1,16) = 4,49 no se puede rechazar la hipótesis de que EJERC no mejora el modelo. Obsérvese que esta F_par es exactamente el cuadrado del valor de t correspondiente al coeficiente de EJERC en el modelo con las tres variables independientes.