Probabilidad condicionada

Probabilidad condicionada

Como la probabilidad está ligada a nuestra ignorancia sobre los resultados de la experiencia, el hecho de que ocurra un suceso, puede cambiar la probabilidad de los demás. El proceso de realizar la historia clínica, explorar y realizar pruebas complementarias ilustra este principio.

La probabilidad de que ocurra el suceso A si ha ocurrido el suceso B se denomina probabilidad condicionada y se define

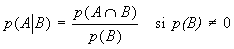
Esta definición es consistente, es decir cumple los axiomas de probabilidad.

Cuando ocurre un suceso cambia el espacio muestral, por eso cambia la probabilidad. A veces es más fácil calcular la probabilidad condicionada teniendo en cuenta este cambio de espacio muestral.

Ejemplo 3:

Una mujer es portadora de la enfermedad de Duchenne ¿Cuál es la probabilidad de que su próximo hijo tenga la enfermedad?

Según las leyes de Mendel, todos los posibles genotipos de un hijo de una madre portadora (xX) y un padre normal (XY) son xX, xY, XX, XY y tienen la misma probabilidad. El espacio muestral es W = {xX, xY, XX, XY}
el suceso A={hijo enfermo} corresponde al genotipo xY, por tanto, según la definición clásica de probabilidad
p(A) = 1/4 = 0,25

La mujer tiene el hijo y es varón ¿qué probabilidad hay de que tenga la enfermedad?

Se define el suceso B = {ser varón} = {xY, XY}
la probabilidad pedida es p(A|B) y aplicando la definición anterior
p(B) = 0,5; A Ç B = {xY}; p(A ÇB) = 0,25; p(A|B) = 0,25/0,5 = 0,5

Si sabemos que es varón, el espacio muestral ha cambiado, ahora es B. Por lo tanto se puede calcular p(A|B) aplicando la definición clásica de probabilidad al nuevo espacio muestral
p(A|B) = 1/2 = 0,5

Ejemplo 4:

Se sabe que el 50% de la población fuma y que el 10% fuma y es hipertensa. ¿Cuál es la probabilidad de que un fumador sea hipertenso?

A = {ser hipertenso} B = {ser fumador}
A Ç B = {ser hipertenso y fumador}
p(A|B) = 0,10/0,50 = 0,20

Obsérvese que los coeficientes falso-positivo y falso-negativo de las pruebas diagnósticas son probabilidades condicionadas.

En general p(A₁ Ç A₂ Ç A₃ ...) = p(A₁) p(A₂|A₁) p(A₃|A₁ Ç A₂) ...
llamado principio de las probabilidades compuestas y especialmente útil para aquellas situaciones en que las probabilidades condicionadas son más fáciles de obtener que las probabilidades de las intersecciones.

Ejemplo 5:

Se sabe por estudios previos que el 0,1% de la población tiene problemas vasculares. Un estudio sobre individuos con problemas vasculares revela que el 20% de ellos son placas de ateroma. Si el 10% de los individuos con placas de ateroma están expuestos a muerte súbita por desprendimiento de trombos ¿qué probabilidad tiene un individuo cualquiera de estar expuesto a muerte súbita por desprendimiento de trombos de una placa de ateroma?

A₁ = {problemas vasculares}; A₂ = {placas de ateroma}; A₃ = {expuesto a muerte súbita por ....}
p(A₁) = 0,001; p(A₂|A₁) = 0,20; p(A₃|A₁ Ç A₂) = 0,1
p(A1 Ç A2 Ç A3) = 0,001 x 0,20 x 0,1 = 0,000002

Ejemplo 6:

Una urna contiene 10 bolas, de las cuales 3 son rojas, 5 verdes y 2 azules. Se extraen al azar 3 bolas. Calcular la probabilidad de que la primera sea azul, y las otras dos verdes.

Definimos A₁ = {la 1ª bola es azul}; A₂ = {la 2ª bola es verde}; A₃= {la 3ª bola es verde}
p(A₁) = 2/10 aplicando la definición clásica de probabilidad, puesto que hay 10 bolas y 2 son verdes.
p(A₂|A₁) = 5/9; si la primera bola extraída es azul, en la urna quedan 9 bolas, 5 de ellas verdes.
p(A₃|A₁ Ç A₂) = 4/8; si la primera bola extraída es azul y la segunda verde en la urna quedan 8 bolas, 4 de ellas verdes.
p(A1 Ç A2 Ç A3) = 2/10 x 5/9 x 4/8 = 1/18