Relación entre los modelos de Poisson y logístico
El intervalo s en el que está definida una variable de Poisson se puede dividir en un conjunto de n subintervalos de tamaño h, cada uno de los cuales es tan pequeño que en ellos sólo puede ocurrir, a lo sumo, un evento, y la probabilidad de que ocurra es la constante l. Por lo tanto, en cada uno de estos intervalos, el número de eventos que ocurren es 0 ó 1, con probabilidades 1 - l y l respectivamente, es decir, es una variable binomial puntual. Una variable de Poisson es, en consecuencia, la suma de n variables binomiales puntuales, es decir, es una variable binomial de parámetros n y l. Como no hay una manera única de elegir los subintervalos, el parámetro n no está bien definido, sin embargo, el tamaño h tiene que ser suficientemente pequeño, por lo tanto n será grande.
En consecuencia, todos los problemas que se pueden plantear con un modelo de Poisson, también se pueden plantear con un modelo logístico, si se dispone de los datos individualizados y, como era de esperar, se obtiene el mismo resultado. Hay que tener en cuenta, no obstante, que el modelo logístico modeliza el odds, mientras que el de Poisson modeliza la probabilidad, por lo tanto los coeficientes sólo coincidirán cuando la probabilidad sea pequeña. Nótese que la inversa no siempre es cierta, hay problemas que se pueden plantear con un modelo logístico y no con un modelo de Poisson, como por ejemplo, un estudio caso-control, en el que la probabilidad no se puede estimar (por tanto, tampoco modelizar) y, sin embargo, sí se puede el odds ratio.
Ejemplo
En un estudio para establecer la eficacia de una vacuna contra la gripe en dos grupos de edad, se mide, durante una semana de invierno, la prevalencia de la misma en dos muestras aleatorias de individuos vacunados y no vacunados en los dos grupos de edad. Se obtienen los siguientes resultados:
| Vacunados | No vacunados | |||
|
Edad |
Total |
Gripe |
Total |
Gripe |
|
20 - 60 |
80 |
3 |
91 |
5 |
|
> 60 |
50 |
5 |
43 |
10 |
El número de individuos con gripe en cada una de las situaciones es una variable de Poisson, para la que se puede plantear un modelo de regresión. Para cada individuo, el tener, o no, gripe, es una variable binomial puntual para la que se puede plantear un modelo logístico.
Para ajustar a un modelo Poisson hay que partir de un archivo como el siguiente:
| EDAD
|
VACUNA
|
TOTAL
|
GRIPE
|
| 0
|
1
|
80
|
3 |
| 1
|
1
|
50
|
5 |
| 0
|
0
|
91
|
5 |
| 1
|
0
|
43
|
10
|
Para ajustar a un modelo logístico hay que crear un archivo en que cada individuo sea una observación. Sería:
|
EDAD
|
VACUNA
|
GRIPE
|
|
|
0
|
1
|
1
|
3 observaciones: individuos vacunados, edad 20-60, con gripe |
|
0
|
1
|
0
|
77 observaciones: individuos vacunados, edad 20-60, sin gripe |
|
1
|
1
|
1
|
5 observaciones: individuos vacunados, edad >60, con gripe |
|
1
|
1
|
0
|
45 observaciones |
|
0
|
0
|
1
|
5 observaciones |
|
0
|
0
|
0
|
86 observaciones |
|
1
|
0
|
1
|
10 observaciones |
|
1
|
0
|
0
|
33 observaciones |
y los ajustes correspondientes:
REGRESION DE POISSON
NOMBRE DE LOS DATOS: eje5pois
VARIABLE DEPENDIENTE: GRIPE
VARIABLE TAMAÑO: TOTAL
NUMERO DE VARIABLES INDEPENDIENTES: 2 A SABER
EDAD VACUNA
NUMERO DE CASOS: 4
NUMERO MAXIMO DE ITERACIONES: 20
CONVERGENCIA OBTENIDA EN 8 ITERACIONES
CASOS QUITADOS POR CONTENER ALGUN VALOR NO ESPECIFICADO: 0
| VARIABLE | ALFA
|
EXP(ALFA)
|
EE.
ALFA |
Ji2
|
p
|
| Const. | -2.79827
|
.06092 |
.37835
|
54.70174
|
.00000
|
| EDAD |
1.28379 |
3.61029
|
.43865
|
8.56527 |
.00357
|
| VACUNA |
-.68495 |
.50412 |
.43865
|
2.43822 |
.11406
|
LOG. MAX. VEROSIMILITUD CON CONSTANTE SOLA= -12.72912
LOG. MAX. VEROSIMILITUD MODELO COMPLETO = -7.18156
Ji-Cuadrado modelo= 11.09511 GL= 2 p= .00410
INTERVALOS
DE CONFIANZA AL 95% DE LOS EXP(ALFA)
EDAD 1.52810 8.52966
VACUNA .21337 1.19102
El riesgo relativo para la vacuna, controlado por la edad, es 0,50412 (la probabilidad de que un individuo vacunado contraiga la gripe es aproximadamente la mitad que la de un individuo sin vacunar) con un intervalo de confianza de (0,21337,1,19102), por lo tanto, no es significativamente distinto de 1.
REGRESION LOGISTICA INCONDICIONAL
NOMBRE DE LOS DATOS: eje52poi
VARIABLE DEPENDIENTE: GRIPE
NUMERO DE VARIABLES INDEPENDIENTES: 2 A SABER
EDAD VACUNA
NUMERO DE CASOS: 264
NUMERO MAXIMO DE ITERACIONES: 20
CONVERGENCIA OBTENIDA EN 7 ITERACIONES
CASOS QUITADOS POR CONTENER ALGUN VALOR NO ESPECIFICADO: 0
| VARIABLE | ALFA
|
EXP(ALFA)
|
EE.
ALFA |
Ji2
|
p
|
| Const. | -2.71567
|
.06616 |
.38959
|
48.58808
|
.00000
|
| EDAD |
1.43544 |
4.20149
|
.46417
|
9.56352 |
.00217
|
| VACUNA |
-.78082 |
.45803 |
.46780
|
2.78598 |
.09094
|
LOG. MAX. VEROSIMILITUD CON CONSTANTE SOLA= -78.09814
LOG. MAX. VEROSIMILITUD MODELO COMPLETO= -71.93247
Ji-Cuadrado modelo= 12.33133 GL= 2 p=
.00230
INTERVALOS DE CONFIANZA AL 95% DE LOS
"ODDS RATIO"
EDAD 1.69159 10.43545
VACUNA .18310 1.14577
El odds ratio para la vacuna es 0,45803 y tampoco es significativamente distinto de 1. En este caso, y como la probabilidad de contraer la gripe no es pequeña, ambos estimadores no coinciden. Sin embargo, si se calcula por ejemplo, la probabilidad de que una persona mayor de 60 años y no vacunada contraiga la gripe con el modelo de Poisson:
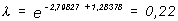
y con el modelo logístico:
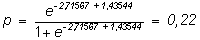
que como se observa, sí coinciden.
|
|
|
|
