Contrastes de hipótesis y estrategias de modelización
Teniendo en cuenta lo anterior los contrastes de hipótesis sobre cada coeficiente se hacen con la prueba de Wald y los contrastes de hipótesis sobre el modelo completo, o sobre un conjunto de coeficientes, con el logaritmo del cociente de verosimilitudes. Por otro lado las estrategias de modelización son exactamente las mismas que las vistas en los capítulos previos.
Supóngase que en las ciudades del ejemplo anterior, la población y los cánceres de piel aparecidos se distribuyen como sigue para distintos grupos de edad:
| Ciudad A | Ciudad B | |||
| Edad | Población | Cáncer | Población | Cáncer |
| 0 – 30 | 120.000 | 3 | 130.000 | 4 |
| 31 – 60 | 200.000 | 7 | 220.000 | 10 |
| > 60 | 30.000 | 8 | 60.000 | 16 |
Estímese, mediante un modelo de Poisson, la razón de densidades de incidencia para ambas ciudades, controlando por la edad.
Para resolverlo con un paquete estadístico (PRESTA), se crea el siguiente archivo con cuatro variables:
| EDAD | CIUDAD | POBLACION | CANCER |
| 1 | 0 | 120.000 | 3 |
| 2 | 0 | 200.000 | 7 |
| 3 | 0 | 30.000 | 8 |
| 1 | 1 | 130.000 | 4 |
| 2 | 1 | 220.000 | 10 |
| 3 | 1 | 60.000 | 16 |
para independizar el resultado de como cambien las densidades de incidencia entre los distintos grupos de edad, se crean a partir de la variable EDAD dos variables indicadoras, EDAD1 y EDAD2, con el primer esquema discutido en regresión lineal y para estudiar la posible interacción entre CIUDAD y EDAD, se crean las variables CIXED1 y CIXED2 con los productos de CIUDAD ´ EDAD1 y CIUDAD ´ EDAD2 respectivamente.
El modelo completo tiene, por lo tanto, cinco variables: CIUDAD, EDAD1, EDAD2, CIXED1 y CIXED2.
El ajuste para este modelo es:
NOMBRE DE
LOS DATOS: eje2pois
VARIABLE DEPENDIENTE:
CANCER
VARIABLE TAMAÑO:
POBLA
NUMERO DE
VARIABLES INDEPENDIENTES: 5 A SABER
CIUDAD
EDAD1 EDAD2 CIXED1
CIXED2
NUMERO DE CASOS: 6
NUMERO MAXIMO
DE ITERACIONES: 20
CONVERGENCIA
OBTENIDA EN 15 ITERACIONES
CASOS QUITADOS
POR CONTENER ALGUN VALOR NO ESPECIFICADO: 0
| VARIABLE | ALFA
|
EXP(ALFA)
|
EE.
ALFA |
Ji2
|
p
|
| Const. | -10.59663
|
.00003
|
.57735
|
336.86620
|
.00000
|
| CIUDAD |
.20764 |
1.23077 |
.76376
|
.07391 |
.78227
|
| EDAD1 |
.33647 |
1.40000 |
.69007
|
.23775 |
.63158
|
| EDAD2 |
2.36712 |
10.66666
|
.67700
|
12.22533 |
.00060
|
| CIXED1 |
.05373 |
1.05520 |
.90895
|
.00349 |
.95139
|
| CIXED2 |
-.20764 |
.81250 |
.87797
|
.05593 |
.80834
|
LOG. MAX. VEROSIMILITUD CON CONSTANTE SOLA= -32.88131
LOG. MAX. VEROSIMILITUD MODELO COMPLETO= -11.39070
Ji-Cuadrado modelo = 42.98121 GL= 5 p=
.00000
El ajuste del modelo, con la prueba del logaritmo del cociente de verosimilitudes es significativo. El primer contraste a realizar es sobre la interacción. Como las variables CIXED1 y CIXED2 son indicadoras y no tienen sentido por sí solas, hay que realizarlo globalmente para las dos con el logaritmo del cociente de verosimilitudes. Se ajusta, por lo tanto, a un modelo sin ellas. El resultado es:
NOMBRE DE LOS DATOS: eje2pois
VARIABLE DEPENDIENTE: CANCER
VARIABLE TAMAÑO: POBLA
NUMERO DE
VARIABLES INDEPENDIENTES: 3 A SABER
CIUDAD EDAD1 EDAD2
NUMERO DE CASOS: 6
NUMERO MAXIMO DE ITERACIONES: 20
CONVERGENCIA OBTENIDA EN 15 ITERACIONES
CASOS QUITADOS POR CONTENER ALGUN VALOR NO
ESPECIFICADO: 0
| VARIABLE | ALFA
|
EXP(ALFA)
|
EE.
ALFA |
Ji2
|
p
|
| Const. | -10.55314
|
.00003
|
.41299
|
652.96970
|
.00000
|
| CIUDAD | .13023
|
1.13909
|
.30131
|
.18681
|
.66947
|
| EDAD1 | .36802
|
1.44486
|
.44909
|
.67153
|
.58226
|
| EDAD2 | 2.23495
|
9.34601
|
.43171
|
26.80163
|
.00000
|
LOG. MAX.
VEROSIMILITUD CON CONSTANTE SOLA= -32.88131
LOG. MAX. VEROSIMILITUD MODELO COMPLETO= -11.47604
Ji-Cuadrado modelo= 42.81053 GL= 3 p=
.00000
Ji-Cuadrado modelo anterior= .17068 GL= 2 p=
.91773
No se puede rechazar la hipótesis nula de no existencia de interacción (p=0,91773), por lo tanto se eliminan dichas variables del modelo. Para este último modelo la matriz estimada de covarianzas de los estimadores es:
MATRIZ DE COVARIANZAS
| Const.
|
CIUDAD
|
EDAD1
|
EDAD2
|
|
| Const. |
.171 |
|||
| CIUDAD | -.050
|
.091 |
||
| EDAD1 | -.143
|
-.000
|
.202
|
|
| EDAD2 | -.136
|
-.013
|
.143
|
.186
|
El próximo contraste a realizar es para las variables EDAD1 y EDAD2, que también tiene que ser global. Se ajusta a un modelo sin ellas y el resultado es:
NOMBRE DE LOS DATOS: eje2pois
VARIABLE DEPENDIENTE: CANCER
VARIABLE TAMAÑO: POBLA
NUMERO DE VARIABLES INDEPENDIENTES: 1 A SABER
CIUDAD
NUMERO DE CASOS: 6
NUMERO MAXIMO DE ITERACIONES: 20
CONVERGENCIA OBTENIDA EN 15 ITERACIONES
CASOS QUITADOS POR CONTENER ALGUN VALOR NO ESPECIFICADO: 0
| VARIABLE | ALFA
|
EXP(ALFA)
|
EE.
ALFA |
Ji2
|
p
|
| Const. | -9.8753
|
.00005 |
.23570
|
1755.39400
|
.00000
|
| CIUDAD |
.3526 |
1.42276
|
.29814
|
1.39869
|
.23503
|
LOG. MAX.
VEROSIMILITUD CON CONSTANTE SOLA= -32.88131
LOG. MAX. VEROSIMILITUD MODELO COMPLETO= -32.16458
Ji-Cuadrado modelo= 1.43345 GL= 1 p=
.22908
Ji-Cuadrado modelo anterior= 41.37708 GL= 2 p= .00000
Obsérvese que esta última estimación coincide con la calculada anteriormente. Con la prueba del logaritmo del cociente de verosimilitudes no se puede rechazar (p=0,00000) que no haya efecto de la edad. En el modelo que contiene la edad, la razón de densidades de incidencia entre las dos ciudades es 1,13909 y no es significativamente distinta de 1 (p=0,66947 con la prueba de Wald). Nótese que la edad es una variable de confusión (con el modelo que sólo contiene la ciudad, la estimación es 1,42276) y por tanto el modelo adecuado para hacer las estimaciones es el que contiene la edad. El intervalo de confianza al 95%, también calculado por el programa, aunque en la salida anterior no se presenta, es (0,631, 2,056).
Para estimar, por ejemplo, con ese modelo la densidad de incidencia para el grupo de mayores de 60 años en la ciudad B, recuérdese que para la ciudad B, CIUDAD=1 y para ese grupo de edad, EDAD1=0 y EDAD2=1, por lo tanto según el modelo:
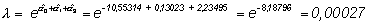
obsérvese que, como el ajuste del modelo es muy bueno, coincide con la estimación que se puede obtener directamente de los datos:
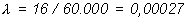
pero el modelo permite, además, calcular un intervalo de confianza para dicha estimación. Para ello hay que calcular:
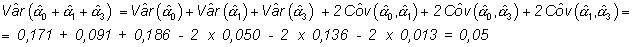
su error estándar es
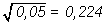
y por lo tanto el intervalo de confianza al 95% es
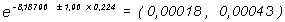
y del mismo modo para los otros grupos de edad y/o la otra ciudad.
Otras lecturas
Silva Ayçaguer L.C., Barroso Utra I.M. Selección algorítmica de modelos en las aplicaciones biomédicas de la regresión múltiple. Medicina Clínica. 2001;116:741-745.
|
|
|
|
|
