Hay ocasiones en que no se dispone de observaciones individuales de los eventos, sino de observaciones agrupadas por intervalos temporales o, incluso, aunque se disponga de las mismas se agrupan para compactar su presentación. Por ejemplo, los datos de mortalidad para un país durante una década se suelen agrupar en intervalos anuales, en las denominadas tablas de vida o actuariales, de modo que no se dispone del tiempo de fallecimiento de cada individuo, sino del número de fallecidos en cada intervalo, en este caso anual.
Supóngase que hay k intervalos, al principio de cada intervalo Ii, existen ni individuos en riesgo, y durante el mismo se producen mi pérdidas y di eventos. Por lo tanto, en el conjunto del intervalo el número de individuos en riesgo es variable, asumiendo que las pérdidas se producen homogéneamente a lo largo del mismo, su número promedio es ni – mi /2 y, en consecuencia, el estimador del riesgo para el intervalo será:
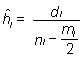
sustituyendo este valor en las fórmulas previas, es decir cambiando en las mismas ni por ni - mi/2 se obtienen los estimadores para la función de supervivencia y su varianza. A este método se le conoce como método actuarial.
Con los datos del ejemplo 1, definiendo intervalos de 5 años, las tablas de vida, obtenidas con el SPSS, son
This subfile contains: 12 observations
Life
Table
Survival
Variable TIEMPO
|
Intrval Start Time |
Number Entrng This Intrval |
Number Wdrawn During Intrval |
Number Exposd to Risk |
Number of Trmnl Events |
Propn Termi- nating |
Propn Sur- viving |
Cumul Propn Surv at End |
Proba- bility Densty |
Hazard Rate |
| ,0 | 12,0 | ,0 | 12,0 | ,0 | ,0000 | 1,0000 | 1,0000 | ,0000 | ,0000 |
| 5,0 | 12,0 | 1,0 | 11,5 | 3,0 | ,2609 | ,7391 | ,7391 | ,0522 | ,0600 |
| 10,0 | 8,0 | 1,0 | 7,5 | 2,0 | ,2667 | ,7333 | ,5420 | ,0394 | ,0615 |
| 15,0 | 5,0 | 1,0 | 4,5 | 2,0 | ,4444 | ,5556 | ,3011 | ,0482 | ,1143 |
| 20,0 | 2,0 | ,0 | 2,0 | 2,0 | 1,0000 | ,0000 | ,0000 | ,0602 | ,4000 |
The median survival time for these data is 15,87
|
Intrval Start Time |
SE
of Cumul Sur- viving |
SE
of Proba- bility Densty |
SE
of Hazard Rate |
| ,0 | ,0000 | ,0000 | ,0000 |
| 5,0 | ,1295 | ,0259 | ,0342 |
| 10,0 | ,1525 | ,0248 | ,0430 |
| 15,0 | ,1526 | ,0288 | ,0774 |
| 20,0 | ,0000 | ,0305 | ,0000 |
Donde la primera columna (“ Intrvl Start Time ”) contiene el tiempo inicial del intervalo; la segunda (“Number Entrng this Intrvl”) el número de individuos en riesgo al inicio del intervalo (ni); la siguiente (“Number Wdrawn this Intrvl”) el número de pérdidas (mi); la siguiente (“ Number Exposd to Risk”) el número de individuos en riesgo en el intervalo (ni – mi /2); la siguiente (“Number of Termnl Events ”) el número de eventos (di); la siguiente (“Propn Terminating”) la función de riesgo (hi) en el intervalo, la siguiente (“ Propn Surviving”) su complementario (1 - hi) que estima la probabilidad de que no ocurra el evento en el intervalo condicionada a que no ocurrió antes; la siguiente (“Cumul Propn Surv at End ”) la función de supervivencia (Si), la siguiente (“Probability Densty”) la función densidad de probabilidad (fi) por unidad de tiempo. Se estima usando las relaciones entre las funciones vistas anteriormente y dividiendo por la anchura del intervalo, es decir, si la anchura del intervalo i fuera bi (en el ejemplo bi = 5 en todos los intervalos)
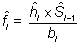
La última columna (“Hazard Rate”) es la función de riesgo por unidad de tiempo, estimada en el punto medio del intervalo por la fórmula
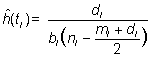
|
|
|
|
|
