Demostraciones de las propiedades de la probabilidad

1) p(A^c) = 1 - p(A)

por ii p(A^c) + p(A) = p(W) Þ p(A^c) = p(W) - p(A) y como por iii p(W)=1 se obtiene 1)

2) A₁ Ì A₂ Þ p(A₁) £ p(A₂)

el suceso B = A₁^c Ç A₂ cumple A₁ È B = A₂ y A₁ Ç B = Æ por lo tanto, según ii) p(A₂) = p(A₁) + p(B) y según i) p(A2) £ p(A1)

3) p(Æ) = 0 por 1) y iii)

4) p(A) £ 1 por 2 y iii)

5) p(A È B) = p(A) + p(B) - p(A Ç B) (Regla general de la adicción)

A È B = A È (A^c ÇB) [1]

En la gráfica se ve claramente, y más generalmente

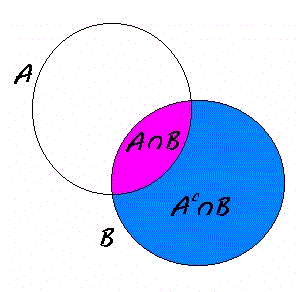
A È (A^c Ç B) = (A È Ac) Ç (A È B) = W Ç (A È B) = A È B

y también A Ç (A^c ÇB) = Æ, por lo tanto aplicando ii a [1]

p(A È B) = p(A) + p(A^c Ç B) [2]

si en [1] se hace la intersección con B

B = (A Ç B) È (A^c Ç B) [3]

pero A Ç B y A^c Ç B son disjuntos

(A Ç B) Ç (A^c Ç B) = A Ç A^c Ç B Ç B = Æ

por lo tanto aplicando ii) a [3]

p(B) = p(A Ç B) + p(A^c Ç B) == p(A^c Ç B) = p(B) - p(A Ç B)

y sustituyéndolo en [2] se obtiene 5

Volver a propiedades de la probabilidad