Problemas de estadística resueltos (1ª parte):
1º Un juego consiste en tirar dos dados. Si la suma de sus caras es mayor o igual a 10 se ganan 300 pts, si está comprendida entre 7 y 9 se ganan 100 pts. y para cualquier otro resultado no se gana nada. ¿Cuál debería ser el precio de la apuesta para que la ganancia esperada de la banca sea de 50 pts?
Solución
El espacio muestral para el problema es W = {(1,1), (1,2), (1,3), ..., (6,6)} con 36 puntos muestrales. Todos los sucesos elementales tiene la misma probabilidad 1/36.
Se define la v.a. X: suma de las dos caras. Esta variable puede tomar los valores 2, 3, 4, ....,12. La tabla con la fdp inducida es
|
x |
Sucesos |
f(x) |
|
2 |
{(1,1)} |
1/36 |
|
3 |
{(1,2), (2,1)} |
2/36 |
|
4 |
{(1,3), (2,2), (3,1)} |
3/36 |
|
5 |
{(1,4), (2,3), (3,2), (4,1)} |
4/36 |
|
6 |
{(1,5), (2,4), (3,3), (4,2), (5,1)} |
5/36 |
|
7 |
{(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)} |
6/36 |
|
8 |
{(2,6), (3,5), (4,4), (5,3), (6,2)} |
5/36 |
|
9 |
{(3,6), (4,5), (5,4), (6,3)} |
4/36 |
|
10 |
{(4,6), (5,5), (6,4)} |
3/36 |
|
11 |
{(5,6), (6,5)} |
2/36 |
|
12 |
{(6,6)} |
1/36 |
La tabla de la función premio es
|
x |
h(x) |
|
2 |
0 |
|
3 |
0 |
|
4 |
0 |
|
5 |
0 |
|
6 |
0 |
|
7 |
100 |
|
8 |
100 |
|
9 |
100 |
|
10 |
300 |
|
11 |
300 |
|
12 |
300 |
Por lo tanto el valor esperado del premio es
en consecuencia, la apuesta debería costar 91,7 + 50 = 141,7 para que la ganancia esperada de la banca sea 50 ptas.
2º La siguiente tabla muestra la fdp para la variable X: número de personas por día que solicitan un tratamiento innecesario en el servicio de urgencias de un pequeño hospital.
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
|
f(x) |
0,01 |
0,1 |
0,3 |
0,4 |
0,1 |
? |
a. Encontrar f(5)
b. Construir F(x)
c. Encontrar p(X£2)
d. Encontrar p(X<2)
e. Encontrar p(X>3)
f. Calcular la media y la varianza
Solución
a. Por la construcción
de las fdps es obvio
que
![]() .
.
Para que se cumpla esta condición es necesario que f(5)=0,09
b.
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
|
f(x) |
0,01 |
0,1 |
0,3 |
0,4 |
0,1 |
0,09 |
|
F(x) |
0,01 |
0,11 |
0,41 |
0,81 |
0,91 |
1 |
c. p(X£2) = F(2) = 0,41
d. p(X<2) = p(X£1) = F(1)=0,11
e. p(X>3) = 1 - p(£3) = 1- F(3) = 1 - 0,81 = 0,19
f.
![]()
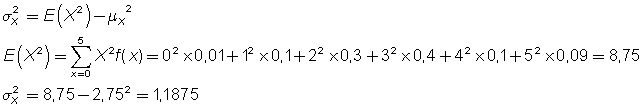
3º Se desarrolla un compuesto para aliviar las migrañas. El fabricante afirma que es efectivo en un 90% de los casos. Se prueba sobre 4 pacientes. Sea X el número de pacientes que obtiene alivio.
a. Encontrar la fdp para X, suponiendo que la afirmación del fabricante sea correcta.
b. Encontrar p(X£1)
c. Si el compuesto no alivia a ninguno de los pacientes ¿es esa una razón para poner en duda la eficacia afirmada por el fabricante? Razonar sobre la base de la probabilidad implicada.
d. Calcular la media. ¿Qué significa en este ejemplo?
Solución
a. Representando por a que un paciente tenga alivio y por n que no lo tenga, el espacio muestral para el problema es W = {aaaa, naaa, anaa, aana, aaan, ..., nnnn}, Si es cierta la afirmación del fabricante p(a)=0,9 y p(n)=0,1
La v.a. X: número de pacientes que tienen alivio puede tomar los valores 0, 1, 2, 3, 4. La tabla con la fdp inducida es
|
x |
Sucesos |
f(x) |
|
0 |
{nnnn} |
0,14 |
|
1 |
{annn, nann, nnan, nnna} |
4x0,9x0,13 |
|
2 |
{aann, anan, anna, naan, nana, nnaa } |
6x0,92x0,12 |
|
3 |
{aaan, aana, anaa, naaa} |
4x0,93x0,1 |
|
4 |
{aaaa} |
0,94 |
b. p(X£1) = f(0) + f(1) = 0,14 + 4x0,9x0,13 = 0,0037
c. La probabilidad de que no alivie a ningún paciente es f(0)=0,0001. Es una probabilidad tan baja que, efectivamente, si ese fuera el resultado hay suficientes razones para poner en duda la afirmación de que alivia al 90% de los pacientes.
d.
![]()
Si se repitiera un número suficientemente grande de veces la experiencia de administrar el fármaco a 4 pacientes, el número promedio de pacientes que experimentarían alivio sería 3,6.
4º Sea X el tiempo de supervivencia en años después de un diagnóstico de leucemia aguda. La fdp para X es f(x) = -x/2 + 1, para 0 < x < 2.
a. Comprobar que es una fdp.
b. Hallar p(X>1)
c. Hallar p(X=1)
d. Hallar p(X³1)
Ayuda: hacerlo todo gráficamente
e. Calcular la media y la varianza (Sólo para iniciados).
Solución
a. La gráfica de la fdp es
|
|
La condición equivalente a |
b.
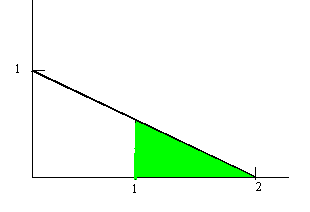
|
Gráficamente, la probabilidad pedida es el área coloreada de verde, por lo tanto se puede calcular también con la fórmula del área del triángulo. Ahora b=1 y para calcular h hay que ver que valor toma la fdp cuando x=1, y = -1/2 + 1 = 1/2. Por lo tanto, la probabilidad es (1x1/2)/2 = 1/4 |
 |
c. Como en toda variable continua la probabilidad de que tome un valor concreto es 0, por lo tanto p(X=1) = 0
d. Obviamente p(X³1) = p(X >1) = 1/4
e. Media
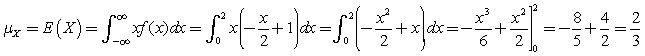
varianza
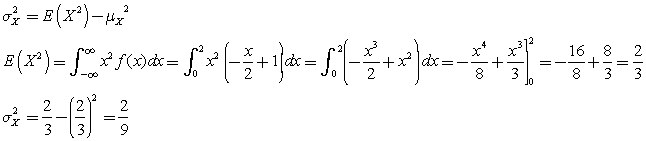
|
|
|
|