Problemas de estadística propuestos (3ª parte):

1º Plantear (y resolver) el contraste de hipótesis adecuado para el problema 2 de la serie anterior: Para evaluar una vacuna para la gripe se selecciona un grupo de 200 individuos de riesgo. Se eligen aleatoriamente a 100 de ellos y se les suministra la vacuna; de ellos 10 pasan la gripe. En los otros 100 pacientes sin vacunar la pasan 20. ¿Hay evidencia de que la vacuna es eficaz?

Solución

H₀: No hay asociación entre la vacuna y la gripe (la vacuna no es eficaz)

Construimos la tabla

Calculamos los valores esperados en H₀

Calculamos el estadístico c²

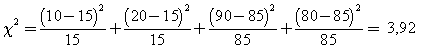
Como el valor crítico de c² es 3,84 rechazamos la H₀ y concluimos que la vacuna es eficaz.

2º Antiguos estudios muestran que el germicida DDT puede acumularse en el cuerpo. En 1965, la concentración media de DDT en las partes grasas del cuerpo en la población española era de 9 ppm. Se espera que como resultado de los controles realizados esta concentración haya disminuido.

a. Construir la hipótesis nula y alternativa para documentar esta afirmación.

b. Explicar en términos prácticos las consecuencias de cometer un error tipo I y un error tipo II.

c. Se realiza el contraste de forma que la potencia para detectar una concentración media de 6 ppm es de 0,8. Explicar en términos prácticos qué significa.

Solución

a. Llamando m_a a la concentración media antes y m_d a la concentración media ahora, las hipótesis se plantean

H₀: m_a = m_d
H₁: m_a > m_d

b. Error tipo I = (rechazar H₀|H₀ cierta) es decir concluir que la concentración ha disminuido, cuando en realidad no ha sido así.
Error tipo II = (aceptar H₀|H₀ falsa) es decir concluir que la concentración no ha disminuido, cuando en realidad si ha disminuido

c. El diseño garantiza que si la concentración media ha disminuido 6 ppm o más el estudio tiene una probabilidad de 0,8 de detectarlo.

3º En un estudio caso-control para estudiar la posible asociación entre estado civil y mortalidad en la UVI se ha encontrado que de 50 personas que murieron 30 eran solteros, mientras que entre 60 que sobrevivieron sólo lo eran 15. Plantear y resolver el contraste. ¿Cuál sería el mejor estimador del efecto?

Solución

H₀: No hay asociación entre el estado civil y la mortalidad

Construimos la tabla

Calculamos los valores esperados en H₀

Calculamos el estadístico c²

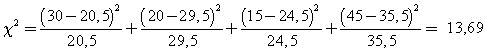
Como el valor crítico de c² es 3,84 rechazamos la H₀ y concluimos que hay asociación. El mejor estimador de la fuerza de la asociación (realmente el único posible de los que hemos visto para este tipo de estudios) es el OR estimado como