Distribución muestral del índice k

El índice k se calcula a partir de muestras, por tanto se obtiene sólo una estimación del verdadero valor del k en la población. Es necesario estudiar su distribución muestral para poder construir intervalos de confianza y realizar contrastes de hipótesis.

En el caso de dos observadores clasificando en K categorías, en la hipótesis de independencia, se puede demostrar que la varianza del kappa estimado es

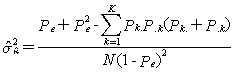
y si se cumplen las condiciones de aproximación de la binomial a la normal, el estadístico se distribuye como una normal tipificada y puede usarse para contrastar la H₀: k = 0 con una región crítica para un contraste lateral z > z_a

Ejemplo : Realizar el contraste de hipótesis H₀: k = 0 para los datos del ejemplo de los reumatólogos. Según la tabla

P_.1=18/80=0.225 P_.2=40/80=0.5

P_.3=22/80=0.275 P_1.=20/80=0.25

P_2.=43/80=0.5375 P_3.=17/80=0.2125

P_e=0.383

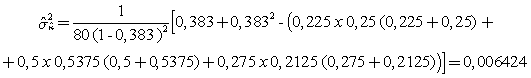
por lo tanto

y no se puede rechazar la hipótesis nula de k = 0.

En general, sin embargo, estos contrastes no tienen mucho interés. El objetivo de un estudio de concordancia no es tanto contrastar si hay más acuerdo que el esperado en la hipótesis de independencia sino cuantificar el mismo. Si un estudio produce un k = 0,1 aunque sea significativamente distinto de 0, revela un acuerdo insignificante. Lo que tiene interés es, por tanto, la estimación por intervalos. Aquí debe señalarse que la varianza anterior se ha obtenido en la hipótesis de independencia entre observadores en cuyo caso k=0, y consecuentemente no sirve para construir intervalos de confianza en la hipótesis de no independencia. En esta hipótesis se puede demostrar que

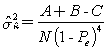
siendo

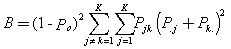
y a partir de esta varianza, un intervalo de confianza aproximado, usando la normalidad asintótica de la distribución de, con un nivel de confianza de 100(1 - a)% es

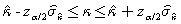
También hay fórmulas, que os ahorro, para la varianza del kappa ponderado. Para el caso de múltiples observadores, aunque hay algunas aproximaciones parciales, no existe todavía una fórmula de uso general para la estimación de su varianza, y se suele usar una técnica muy general para construir intervalos de confianza para estadísticos de distribución muestral desconocida que es la denominada "técnica jackknife", introducida por Quenouille y que se puede aplicar al índice kappa.

Referencias

Abraira V., Pérez de Vargas A. (1999). Generalization of the kappa coefficient for ordinal categorical data, multiple observers and incomplete designs. Qüestiió 23: 561-571