Comparación de medias
La
hipótesis nula
H0:
m1 - m2
= d0
Generalmente d0=0
Hay
3 situaciones distintas:
1º ![]() conocidos (poco
frecuente).
conocidos (poco
frecuente).
2º ![]() desconocidos pero
iguales.
desconocidos pero
iguales.
3º ![]() desconocidos pero
distintos.
desconocidos pero
distintos.
Los estadísticos son distintos (z en 1 y t en 2 y 3) pero el procedimiento es el mismo. En los 3 casos se supone que las muestras son independientes; si no lo fueran hay otro estadístico (t pareada).
Todos asumen normalidad. Si no se cumpliera hay que usar los llamados test no paramétricos.
Ejemplo
En
un ensayo clínico para evaluar un hipotensor se compara un grupo placebo con el
grupo tratado. La variable medida es la disminución de la presión sistólica y
se obtiene: grupo placebo n = 35; ![]() = 3,7 mm de Hg. y s2 = 33,9; grupo tratado n = 40;
= 3,7 mm de Hg. y s2 = 33,9; grupo tratado n = 40; ![]() = 15,1 mm de Hg. y s2
= 12,8. ¿Es eficaz el tratamiento?
= 15,1 mm de Hg. y s2
= 12,8. ¿Es eficaz el tratamiento?
Se
trata de un contraste sobre diferencias de medias
H0: mT
- mP
= 0
H1:
mT
- mP> 0
Como no conocemos las varianzas, para realizarlo debemos
decidir si son iguales o distintas, para ello se plantea el contraste
H0: ![]()
H1: ![]()
El
estadístico es ![]() ,
para el que p<0,05, en consecuencia rechazamos la H0 y concluimos
que las varianzas son distintas. Por lo tanto usaríamos la t para
varianzas distintas. Haciendo los cálculos t=-10,2 p<0,05 rechazamos
la H0 y concluimos que las medias son distintas.
,
para el que p<0,05, en consecuencia rechazamos la H0 y concluimos
que las varianzas son distintas. Por lo tanto usaríamos la t para
varianzas distintas. Haciendo los cálculos t=-10,2 p<0,05 rechazamos
la H0 y concluimos que las medias son distintas.
Nota: Para hacerlo con un paquete estadístico, p.e. el SPSS, deberíamos crear un archivo con 2 variables: Trata (con un código distinto para cada grupo, p.e. 0 para placebo y 1 para tratado) y Diferen con la diferencia de presión arterial para cada individuo al acabar el estudio y al empezar. Originalmente en el archivo podría haber una variable con la presión al empezar y otra al acabar y se crearía la diferencia con la opción: Transformar ---> Calcular. Para calcular la t desplegamos los menús que se ven en la gráfica:
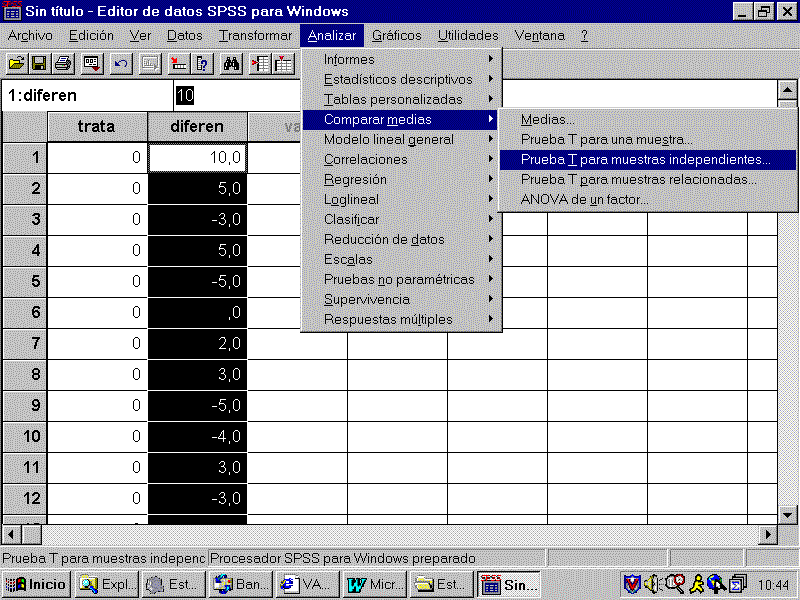
Y el programa calcula la t para varianzas iguales y distintas y realiza el contraste para las varianzas. Para el contraste sobre las varianza el SPSS no usa la prueba descrita más arriba, sino la de Levene que no asume normalidad y se puede usar para comparar varias varianzas.
Estadísticos del grupo
| TRATA | N | Media | Desviación típ. | Error típ. de la media | |
| DIFEREN | 0 | 35 | 3,729 | 5,666 | ,958 |
| 1 | 40 | 15,075 | 3,576 | ,565 |
Prueba de muestras independientes
| Prueba de Levene para la igualdad de varianzas | Prueba T para la igualdad de medias | |||||||||
| F | Sig. | t | gl | Sig. (bilateral) | Diferencia de medias | Error típ de la diferencia | Intervalo de confianza para la diferencia | |||
| Inferior | Superior | |||||||||
| DIFEREN | Se han asumido varianzas iguales | 10,431 | ,002 | -10,503 | 73 | ,000 | -11,346 | 1,080 | -13,500 | -9,193 |
| No se han asumido varianzas iguales | -10,201 | 55,909 | ,000 | -11,346 | 1,112 | -13,575 | -9,118 | |||
¿Qué nos está diciendo este resultado? Que si el tratamiento fuera igual de eficaz que el placebo, la probabilidad de haber obtenido una diferencia entre ambos como la que hemos encontrado o mayor es muy pequeña (<0,000) ¿Bastaría esto para convencernos de que debemos tratar con este tratamiento?
|
|
|
|
|
