Contrastes de hipótesis en un anova de dos vías

Supóngase el primer factor de efectos fijos y el segundo de efectos aleatorios, lo que no supone ninguna perdida de generalidad, ya que el orden de los factores es arbitrario.

MS	Valor esperado
MSA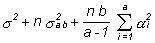
MSB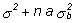
MSAB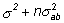
MSE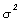

Se contrastan la interacción y el factor aleatorio con el término de error, si la interacción fuera significativa no tiene sentido contrastar el efecto fijo y si no lo fuera, el efecto fijo se contrasta con el término de interacción o con el promedio de interacción y error.